题目内容
已知函数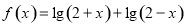 .
.
(1)求函数 的定义域;
的定义域;
(2)若不等式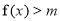 有解,求实数
有解,求实数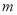 的取值范围.
的取值范围.
(1) ;(2)
;(2) .
.
【解析】
试题分析:(1)由对数有意义,得 可求定义域;(2)不等式
可求定义域;(2)不等式 有解
有解
 ,由
,由 ,可得
,可得 的最大值为
的最大值为 ,所以
,所以 。
。
试题解析:(1) 须满足
须满足 ,∴
,∴ ,
,
∴所求函数的定义域为 .
.
(2)∵不等式 有解,∴
有解,∴
 =
=
令 ,由于
,由于 ,∴
,∴
∴ 的最大值为
的最大值为 ∴实数
∴实数 的取值范围为
的取值范围为 .
.
考点:对数性质、对数函数性、不等式有解问题。

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
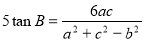 , 则
, 则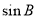 的值是 .
的值是 .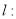
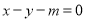 经过抛物线
经过抛物线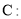
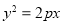 (
(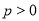 )的焦点,
)的焦点,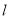 与
与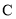 交于
交于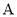 、
、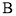 两点.若
两点.若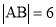 ,则
,则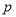 的值为( )
的值为( )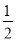 B.
B.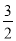 C.
C.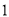 D.
D.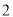
 ,
, 满足约束条件
满足约束条件 ,则目标函数
,则目标函数 的取值范围为( )
的取值范围为( ) B.
B. C.
C. D.
D.
 ,
, ,若
,若 ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 满足
满足 ,则当
,则当 时,数列
时,数列 的前
的前 项和最大.
项和最大. 时,函数
时,函数 的最小值是( )
的最小值是( ) ,
, ,
, 的方差为
的方差为 ,则数据
,则数据 ,
, ,
, 的方差是 .
的方差是 . )上恒成立,求a的最小值.
)上恒成立,求a的最小值.