题目内容
18．已知命题p：方程x2+ax+2a=0有解；命题q：函数f（x）=$\left\{\begin{array}{l}{（\frac{1}{2}）^{x}-2，x≤0}\\{（2-a）x-1，x＞0}\end{array}\right.$在R上是单调函数．（1）当命题q为真命题时，求实数a的取值范围；
（2）当p为假命题，q为真命题时，求实数a的取值范围．
分析 （1）根据分段函数的单调性的性质进行求解即可，
（2）根据p为假命题，q为真命题时，求出对应的a的范围，进行求解即可．
解答 解：（1）若q为真命题，则由题意得$\left\{{\begin{array}{l}{2-a＜0}\\{{{（\frac{1}{2}）}^0}-2≥（2-a）•0}\end{array}}\right.$，得a＞2．…（6分）
（2）命题p为真命题时实数a满足：△=a2-4•2a≥0，得a≥8，a≤0，…（9分）
若p为假命题，q为假命题时，则实数a满足$\left\{{\begin{array}{l}{0＜a＜8}\\{a＞2}\end{array}}\right.$，得2＜a＜8． …（13分）
点评 本题主要考查命题的真假判断，涉及复合命题的真假关系，求出命题为真命题的等价条件是解决本题的关键．
练习册系列答案
相关题目
8．等差数列3，1，-1，-3，…，-93的项数为（ ）
| A． | 52 | B． | 51 | C． | 49 | D． | 50 |
9．
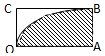如图，长方形的四个顶点坐标为O（0，0），A（4，0），B（4，2），C（0，2），曲线y=$\sqrt{x}$经过点B，现将质点随机投入长方形OABC中，则质点落在图中阴影部分的概率为（ ）
如图，长方形的四个顶点坐标为O（0，0），A（4，0），B（4，2），C（0，2），曲线y=$\sqrt{x}$经过点B，现将质点随机投入长方形OABC中，则质点落在图中阴影部分的概率为（ ）| A． | $\frac{2}{3}$ | B． | $\frac{3}{4}$ | C． | $\frac{4}{5}$ | D． | $\frac{5}{6}$ |
6．设a=0.60.6，b=0.61.5，c=1.50.6，则a，b，c的大小关系（ ）
| A． | a＜b＜c | B． | a＜c＜b | C． | b＜a＜c | D． | b＜c＜a |
10．已知等比数列{an}中的各项都是正数，且${a_1}，\frac{1}{2}{a_3}，2{a_2}$成等差数列，则$\frac{{{a_9}+{a_{10}}+{a_{13}}}}{{{a_7}+{a_8}+{a_{11}}}}$=（ ）
| A． | $1+\sqrt{2}$ | B． | $1-\sqrt{2}$ | C． | $3+2\sqrt{2}$ | D． | $3-2\sqrt{2}$ |
7．将函数f（x）=2sin2x的图象向左平移$\frac{π}{12}$个单位后得到函数g（x）的图象，若函数g（x）在区间[0，$\frac{a}{3}$]和[2a，$\frac{7π}{6}$]上均单调递增，则实数a的取值范围是（ ）
| A． | [$\frac{π}{3}$，$\frac{π}{2}$] | B． | [$\frac{π}{6}$，$\frac{π}{2}$] | C． | [$\frac{π}{6}$，$\frac{π}{3}$] | D． | [$\frac{π}{4}$，$\frac{3π}{8}$] |
8．在以下关于向量的命题中，不正确的是（ ）
| A． | 若向量$\overrightarrow a=（x，y）$，向量$\overrightarrow b=（-y，x）$（xy≠0），则$\overrightarrow a⊥\overrightarrow b$ | |
| B． | 若四边形ABCD为菱形，则$\overrightarrow{AB}=\overrightarrow{DC}\;，\;且|\overrightarrow{AB}|=|\overrightarrow{AD}|$ | |
| C． | 点G是△ABC的重心，则$\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow 0$ | |
| D． | △ABC中，$\overrightarrow{AB}$和$\overrightarrow{CA}$的夹角等于A |