题目内容

2．实数x，y满足$\left\{{\begin{array}{l}{x-y+1≥0}\\{x+y-3≥0}\\{2x+y-7≤0}\end{array}}\right.$，若x-2y≥m恒成立，则实数m的取值范围是（　　）
A．（-∞，-3]B．（-∞，-4]C．（-∞，6]D．[0，6]

分析 首先画出可行域，由4x-y≥m恒成立，即求4x-y的最小值，设z=4x-y，利用其几何意义求最小值．

解答 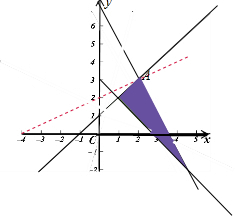解：x，y满足的平面区域如图：设z=x-2y，则y=$\frac{1}{2}$x-$\frac{1}{2}$z
当经过图中的A时z最小，由$\left\{\begin{array}{l}{x-y+1=0}\\{2x+y-7=0}\end{array}\right.$得到A（2，3），
所以z的最小值为2-2×3=-4；
所以实数m的取值范围是（-∞，-4]；
故选：B．

点评 本题考查了简单线性规划问题；正确画出可行域，将恒成立问题求参数范围问题，转化为求4x-y的最小值．

练习册系列答案
相关题目
12．如图，已知矩形ABCD中，AB=2$\sqrt{2}$，AD=$\sqrt{2}$，M为DC的中点，将△ADM沿AM折起，使得平面ADM⊥平面ABCM．

（1）求证AD⊥BM．；
（2）若E是线段DB的中点，求二面角E-AM-D的余弦值．
13．已知集合A={x|$\frac{1}{3}≤（\frac{1}{3}）^{x-1}≤9$}，集合B={x|log2x＜3}，集合C={x|（x-a）[x-（a+1）≤0}，U=R．
（1）求集合A∩B，（∁UB）∪A；
（2）若A∪C=A，求实数a的取值范围．
10．已知圆M：（x-3）2+（y-3）2=4，E，F分别为圆内接正△ABC的边AB，BC的中点，当△ABC绕圆心M转动时，则$\overrightarrow{ME}•\overrightarrow{OF}$（O为坐标原点）的取值范围是（　　）
A．$[{-\frac{1}{2}-6\sqrt{2}，-\frac{1}{2}+6\sqrt{2}}]$B．[-6，6]C．$[{-\frac{1}{2}-3\sqrt{2}，-\frac{1}{2}+3\sqrt{2}}]$D．[-4，4]
17．直线（m2+1）x-2my=1的倾斜角的取值范围为$[{\frac{π}{4}，\frac{3π}{4}}]$．
7．《九章算术》中有一个“两鼠穿墙”问题：“今有垣（墙，读音）厚五尺，两鼠对穿，大鼠日（第一天）一尺，小鼠也日（第一天）一尺．大鼠日自倍（以后每天加倍），小鼠日自半（以后每天减半）．问何日相逢，各穿几何？”
在两鼠“相逢”时，大鼠与小鼠“穿墙”的“进度”之比是59：26．
14．已知数列{an}的前两项均为1，前n项和为Sn，若{2nan}为等差数列，则Sn=$\frac{{2}^{n+1}-n-2}{{2}^{n-1}}$．．
11．已知双曲线$\frac{x^2}{9}-\frac{y^2}{m}$=1的一条渐近线方程为y=±$\frac{4}{3}$x，则实数m等于16．
12．命题“?x0∈∁RQ，x03∈Q”的否定是（　　）
A．?x0∉∁RQ，x03∈QB．?x0∈∁RQ，x03∈QC．?x∉∁RQ，x3∈QD．?x∈∁RQ，x3∉Q

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网