题目内容
【题目】已知函数![]() .
.
(1)若函数![]() 的最小值是
的最小值是![]() ,且c=1,
,且c=1,![]() ,求F(2)+F(-2)的值;
,求F(2)+F(-2)的值;
(2)若a=1,c=0,且![]() 在区间(0,1]上恒成立,试求b的取值范围.
在区间(0,1]上恒成立,试求b的取值范围.
【答案】(1)8;(2)[-2,0]
【解析】
(1)由函数f(x)的最小值是f(﹣1)=0,且c=1,解得a,b的值,得到f(x)解析式代入到F(x)中,计算出F(2)+F(﹣2)的值;
(2)由a=1,c=0,则f(x)=x2+bx,把问题﹣1≤f(x)≤1在区间(0,1]上恒成立转化为﹣x![]() b
b![]() x在区间(0,1]上恒成立,研究﹣x
x在区间(0,1]上恒成立,研究﹣x![]() 和
和![]() x在(0,1]的单调性求出最值,从而得到b的取值范围.
x在(0,1]的单调性求出最值,从而得到b的取值范围.
(1)由已知c=1,a-b+c=0,且-![]() =-1,解得a=1,b=2,∴f(x)=(x+1)2.
=-1,解得a=1,b=2,∴f(x)=(x+1)2.
∴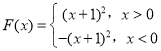 ,∴F(2)+F(-2)=(2+1)2+[-(-2+1)2]=8.
,∴F(2)+F(-2)=(2+1)2+[-(-2+1)2]=8.
(2)f(x)=x2+bx,原命题等价于-1≤x2+bx≤1在(0,1]上恒成立,
即b≤![]() -x且b≥-
-x且b≥-![]() -x在(0,1]上恒成立.
-x在(0,1]上恒成立.
又y=![]() -x单调递增,故最小值为0,y=-
-x单调递增,故最小值为0,y=-![]() -x=-(
-x=-(![]() +x)
+x)![]() 当且仅当
当且仅当![]() 取等.
取等.
∴-2≤b≤0.故b的取值范围是[-2,0].

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案【题目】某公司需要对所生产的![]() 三种产品进行检测,三种产品数量(单位:件)如下表所示:
三种产品进行检测,三种产品数量(单位:件)如下表所示:
产品 | A | B | C |
数量(件) | 180 | 270 | 90 |
采用分层抽样的方法从以上产品中共抽取6件.
(1)求分别抽取三种产品的件数;
(2)将抽取的6件产品按种类![]() 编号,分别记为
编号,分别记为![]() ,现从这6件产品中随机抽取2件.
,现从这6件产品中随机抽取2件.
(ⅰ)用所给编号列出所有可能的结果;
(ⅱ)求这两件产品来自不同种类的概率.
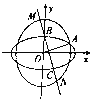
【题目】已知椭圆![]() ,抛物线
,抛物线![]() 的焦点均在
的焦点均在![]() 轴上,
轴上, ![]() 的中心和
的中心和![]() 的顶点均为原点
的顶点均为原点![]() ,从
,从![]() ,
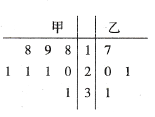
, ![]() 上分别取两个点,将其坐标记录于下表中:
上分别取两个点,将其坐标记录于下表中:
| 3 | -2 | 4 |
|
|
| 0 | -4 |
|
(1)求![]() 的标准方程;
的标准方程;
(2)若直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,且线段
,且线段![]() 的垂直平分线过定点
的垂直平分线过定点![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.