题目内容
7.已知函数f(x)=asinx+bcosx.(1)当f($\frac{π}{4}$)=$\sqrt{2}$,且f(x)max=$\sqrt{10}$时,求a、b的值;
(2)当f($\frac{π}{3}$)=1,且f(x)min=k时,求k的取值范围.
分析 (1)由辅助角公式,将f(x)=$\sqrt{{a}^{2}+{b}^{2}}$sin(x+φ),sinφ=$\frac{b}{\sqrt{10}}$,cosφ=$\frac{a}{\sqrt{10}}$,求得$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{10}$,f($\frac{π}{4}$)=$\sqrt{2}$,利用两角和的正弦公式化简求得
sin$\frac{π}{4}$cosφ+cos$\frac{π}{4}$sinφ=$\frac{\sqrt{5}}{5}$,代入求得a=3 b=-1 或a=-1 b=3,
(2))f($\frac{π}{3}$)=1得$\frac{\sqrt{3}}{2}a+\frac{1}{2}b=1$,化简利用二次函数的性质求得 a=$\frac{\sqrt{3}}{2}$时 K2最小,最小K为1,K≥1.
解答 解:(1)f(x)=asinx+bcosx=$\sqrt{{a}^{2}+{b}^{2}}$sin(x+φ),
∴$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{10}$,f($\frac{π}{4}$)=$\sqrt{2}$,
f($\frac{π}{4}$)=2,可得a+b=2,
联立解得:a=3 b=-1 或a=-1 b=3;
(2)f($\frac{π}{3}$)=1,$\frac{\sqrt{3}}{2}a+\frac{1}{2}b=1$,
∴a2+b2=K2(K为负数),
∴K2=a2+b2=a2+4(1-$\frac{\sqrt{3}}{2}a$)2=4a2-4$\sqrt{3}$a+4≥1,
当 a=$\frac{\sqrt{3}}{2}$时 K2最小,最小K2为1,
K≤-1.
点评 本题考查辅助角公式,求函数的解析式、两角和的正弦公式和二次函数的性质,属于中档题.

| A. | 数列4,7,3,4的首项是4 | |
| B. | 数列{an}中,若a1=3,则从第2项起,各项均不等于3 | |
| C. | 数列-1,0,1,2与数列0,1,2,-1不相同 | |
| D. | 数列中的项不能是三角形 |
| A. | 2n>2n+1 | B. | 2n+1>2n+1 | C. | 2n+2>2n+5 | D. | 2n+3>2n+7 |
| A. | 必要非充分条件 | B. | 充要条件 | ||
| C. | 充分非必要条件 | D. | 既非充分也非必要条件 |
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | $\sqrt{5}$ | D. | $\sqrt{6}$ |
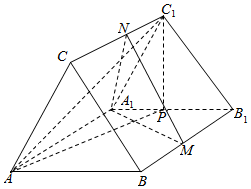 如图,直三棱柱ABC-A1B1C1中,△ABC是正三角形,AB=AA1,M是BB1的中点,P是A1B1的中点,N是线段CC1上的动点.
如图,直三棱柱ABC-A1B1C1中,△ABC是正三角形,AB=AA1,M是BB1的中点,P是A1B1的中点,N是线段CC1上的动点.