题目内容
定义域为 的奇函数
的奇函数 满足
满足 ,且当
,且当 时,
时,  .
.
(Ⅰ)求 在
在 上的解析式;
上的解析式;
(Ⅱ)当 取何值时,方程
取何值时,方程 在
在 上有解?
上有解?
(Ⅰ)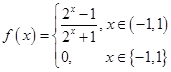 ;(Ⅱ)
;(Ⅱ)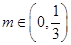 .
.
解析试题分析:(Ⅰ)先设自变量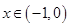 ,先求出
,先求出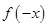 的表达式,然后根据奇函数的定义
的表达式,然后根据奇函数的定义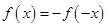 即可求出函数
即可求出函数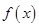 在
在 上的解析式,对于其它点出的函数值,则根据其它条件确定;(Ⅱ)把问题进行适当转化,方程
上的解析式,对于其它点出的函数值,则根据其它条件确定;(Ⅱ)把问题进行适当转化,方程 在
在 上有解
上有解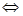
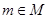 (其中
(其中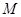 为函数
为函数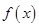 在
在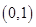 上的值域),只需根据不等式的性质或函数的单调性确定函数
上的值域),只需根据不等式的性质或函数的单调性确定函数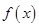 在
在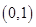 上的值域就可以确定实数
上的值域就可以确定实数 的取值范围了.
的取值范围了.
试题解析:(Ⅰ)当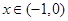 时,
时,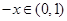 ,由
,由 为
为 上的奇函数,
上的奇函数,
得 ,
,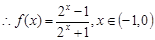 ,又有奇函数得
,又有奇函数得
又 满足
满足
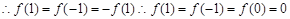
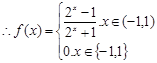 5分
5分
(Ⅱ)当
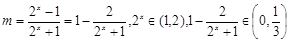 即
即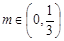 10分
10分
考点:函数的奇偶性、不等式的性质

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
 的一部分,栏栅与矩形区域的边界交于点
的一部分,栏栅与矩形区域的边界交于点 ,交曲线于点
,交曲线于点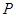 ,设
,设 .
.
 (
( 为坐标原点)的面积
为坐标原点)的面积 表示成
表示成 的函数
的函数 ;
; 处,
处, 的值及
的值及 是同时符合以下性质的函数
是同时符合以下性质的函数 组成的集合:
组成的集合: ,都有
,都有 ;②
;② 上是减函数.
上是减函数. 和
和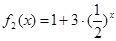 (
( )是否属于集合
)是否属于集合 ,若不等式
,若不等式 对任意的
对任意的 总成立,求实数
总成立,求实数 的取值范围.
的取值范围. .
.
 成立的
成立的 的取值范围;
的取值范围; ,
, ,求实数
,求实数 的取值范围.
的取值范围.
 ,解不等式
,解不等式 ;
; 时,若
时,若
 ,使得不等式
,使得不等式 成立,求实数
成立,求实数 的取值范围.
的取值范围. .
. 时,求曲线
时,求曲线 在原点处的切线方程;
在原点处的切线方程; 时,讨论函数
时,讨论函数 在区间
在区间 上的单调性;
上的单调性; 对任意
对任意 成立.
成立. ,
, .
. 的单调区间;
的单调区间; 时,函数
时,函数 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; 满足
满足 ,求证:
,求证: .
.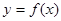 是定义域为
是定义域为 的奇函数,且当
的奇函数,且当 时,
时, ,(
,( 。
。 的值;并求函数
的值;并求函数
 上是增函数。
上是增函数。 (m为常数0<m<1),且数列{f(
(m为常数0<m<1),且数列{f( )}是首项为2,公差为2的等差数列.
)}是首项为2,公差为2的等差数列. =
= 时,求数列{
时,求数列{ ;
; =
= ,如果{
,如果{