题目内容
7.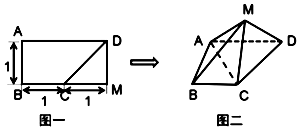 将如图一的矩形ABMD沿CD翻折后构成一四棱锥M-ABCD(如图二),若在四棱锥M-ABCD中有MA=$\sqrt{3}$.
将如图一的矩形ABMD沿CD翻折后构成一四棱锥M-ABCD(如图二),若在四棱锥M-ABCD中有MA=$\sqrt{3}$.(1)求证:AC⊥MD;
(2)求四棱锥M-ABCD的体积.
分析 (1)推导出MD⊥MA,MD⊥MC,从而MD⊥平面MAC,由此能证明AC⊥MD.
(2)取CD的中点F,连接MF,推导出AC⊥CD,从而AC⊥MD,进而AC⊥平面MCD,MF⊥平面ABCD,由此能求出四棱锥M-ABCD的体积.
解答 证明:(1)在△MAD中,$MA=\sqrt{3}$,MD=1,AD=2,
∴MA2+MD2=AD2,∴MD⊥MA,
又∵MD⊥MC,∴MD⊥平面MAC,
∴AC⊥MD.
解:(2)取CD的中点F,连接MF,
如图二,在△ACD中,$CD=AC=\sqrt{2}$,AD=2,
∴AC2+CD2=AD2,∴AC⊥CD,
由(1)可知MD⊥平面MAC,
∴AC⊥MD,∴AC⊥平面MCD,∴AC⊥MF,
在△MCD中,MC=MD=1,∴MF⊥CD,$MF=\frac{{\sqrt{2}}}{2}$,
∴MF⊥平面ABCD,
∴${V_{M-ABCD}}=\frac{1}{3}{S_{四边形ABCD}}×MF=\frac{1}{3}×[\frac{1}{2}×(1+2)×1]×\frac{{\sqrt{2}}}{2}=\frac{{\sqrt{2}}}{4}$.
点评 本题考查线线垂直的证明,考查四棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
18.在△ABC中,角A、B、C所对的边长分别为a、b、c,$C=\frac{π}{3}$,若$\overrightarrow{OD}=a\overrightarrow{OE}+b\overrightarrow{OF}$,且D、E、F三点共线(该直线不经过O点),则△ABC周长的最小值是( )
| A. | $\frac{1}{2}$ | B. | $\frac{5}{4}$ | C. | $\frac{3}{2}$ | D. | $\frac{9}{4}$ |
15.已知集合A={0,1,2,3,4},集合B={x|x=2n,n∈A},则A∩B=( )
| A. | {0} | B. | {0,2,4} | C. | {2,4} | D. | {0,2} |
16.设D、E、F分别为△ABC三边BC、CA、AB的中点,则$\overrightarrow{DA}$+2$\overrightarrow{EB}$+3$\overrightarrow{FC}$=( )
| A. | $\frac{1}{2}$$\overrightarrow{AD}$ | B. | $\frac{3}{2}$$\overrightarrow{AD}$ | C. | $\frac{1}{2}$$\overrightarrow{AC}$ | D. | $\frac{3}{2}$$\overrightarrow{AC}$ |
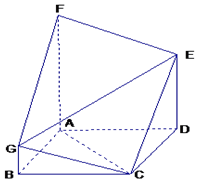 如图,多面体ABCDEFG中,四边形ABCD是正方形,FA⊥平面ABCD,
如图,多面体ABCDEFG中,四边形ABCD是正方形,FA⊥平面ABCD,