题目内容
15．已知集合A={0，1，2，3，4}，集合B={x|x=2n，n∈A}，则A∩B=（ ）| A． | {0} | B． | {0，2，4} | C． | {2，4} | D． | {0，2} |
分析 根据题意求出集合B，再根据交集的定义写出A∩B．
解答 解：集合A={0，1，2，3，4}，
集合B={x|x=2n，n∈A}={0，2，4，6，8}，
则A∩B={0，2，4}．
故选：B．
点评 本题考查了集合的化简与运算问题，是基础题．
练习册系列答案
相关题目
5．在△ABC中，AB=2，AC=3，$\overrightarrow{AB}•\overrightarrow{BC}=1$，则$|\overrightarrow{BC}|$=（ ）
| A． | $\sqrt{7}$ | B． | $\sqrt{3}$ | C． | 2$\sqrt{2}$ | D． | $\sqrt{23}$ |
20．已知函数$f（x）=\left\{\begin{array}{l}{2^x}-a，x≤1\\-x+a，x＞1\end{array}\right.$，则“函数f（x）有两个零点”成立的充分不必要条件是a∈（ ）
| A． | （0，2] | B． | （1，2] | C． | （1，2） | D． | （0，1] |
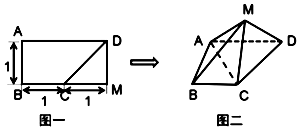将如图一的矩形ABMD沿CD翻折后构成一四棱锥M-ABCD（如图二），若在四棱锥M-ABCD中有MA=$\sqrt{3}$．
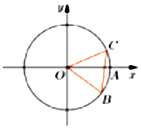如图，圆O与x轴正半轴交点为A，点B，C在圆O上，圆C在第一象限，且B（$\frac{4}{5}$，-$\frac{3}{5}$），∠AOC=α，BC=1，则cos（$\frac{5π}{6}$-α）=-$\frac{3}{5}$．