题目内容
17.将甲、乙、丙、丁四名学生分到三个不同的班,每个班至少分到一名学生,则不同的分法的总数是36.(用数字作答)分析 本题是一个分步计数问题,先选两个元素作为一个元素,问题变为三个元素在三个位置全排列,得到结果.
解答 解:由题意知本题是一个分步计数问题,
4位同学分到三个不同的班级,每个班级至少有一位同学,先选两个人作为一个整体,问题变为三个元素在三个位置全排列,
共有C42A33=36种结果,
故答案为:36.
点评 本题考查分步计数原理,是一个基础题,也是一个易错题,因为如果先排三个人,再排最后一个人,则会出现重复现象,注意不重不漏.

练习册系列答案
相关题目
8.如图是一个算法的流程图,则最后输出的S值为( )


| A. | -1 | B. | -4 | C. | -9 | D. | -16 |
12.直线$ρcosθ=\frac{1}{2}$被圆ρ=1所截得的弦长为( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 4 |
7.设D、E、F分别为△ABC三边BC、CA、AB的中点,则$\overrightarrow{DA}$+$\overrightarrow{EB}$+$\overrightarrow{FC}$=( )
| A. | $\frac{1}{2}$$\overrightarrow{DA}$ | B. | $\frac{1}{3}$$\overrightarrow{DA}$ | C. | $\frac{1}{4}$$\overrightarrow{DA}$ | D. | $\overrightarrow{0}$ |
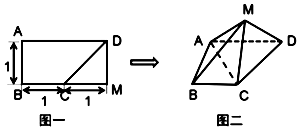 将如图一的矩形ABMD沿CD翻折后构成一四棱锥M-ABCD(如图二),若在四棱锥M-ABCD中有MA=$\sqrt{3}$.
将如图一的矩形ABMD沿CD翻折后构成一四棱锥M-ABCD(如图二),若在四棱锥M-ABCD中有MA=$\sqrt{3}$.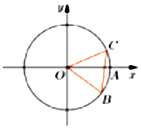 如图,圆O与x轴正半轴交点为A,点B,C在圆O上,圆C在第一象限,且B($\frac{4}{5}$,-$\frac{3}{5}$),∠AOC=α,BC=1,则cos($\frac{5π}{6}$-α)=-$\frac{3}{5}$.
如图,圆O与x轴正半轴交点为A,点B,C在圆O上,圆C在第一象限,且B($\frac{4}{5}$,-$\frac{3}{5}$),∠AOC=α,BC=1,则cos($\frac{5π}{6}$-α)=-$\frac{3}{5}$.