��Ŀ����
18���������Ǿ�������IJ������������˹����ͥ�γ��Ѳ�����һ��ʱ�У�����ʹ�÷��ã�����������ʹ���������࣬��֧���ķ��õ����������٣�һֱ�ǹ���һ��dz����ĵ����⣮ij�������۹�˾����һ�γ������ˣ���ͳ�Ƶó�ij���ʹ������x����֧�����ܷ���y����Ԫ�������µ��������ϣ�| ʹ������x | 2 | 3 | 4 | 5 | 6 |
| �ܷ���y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
1���Իع鷽��$\stackrel{��}{y}$=$\stackrel{��}{b}$x+$\stackrel{��}{a}$��
2����ʹ������Ϊ10��ʱ������ʹ���ܷ����Ƕ��٣�
�����ع�ֱ�ߵ�б�ʺͽؾ����С���˷����ƹ�ʽ�ֱ�Ϊ��$\stackrel{��}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$��$\stackrel{��}{a}$=$\overline{y}$-$\stackrel{��}{b}$$\overline{x}$��
���� ��1�������ݴ��빫ʽ��������С���˷���ع鷽�̵�ϵ�����ɵûع�ֱ�߷��̣�
��2����x=10����ع鷽�̵�yֵ����ΪԤ��������
��� �⣺��1��$\overline{x}$=4��$\overline{y}$=5��$\sum_{i=1}^{5}$xi2=90��$\sum_{i=1}^{5}$xiyi=112.3��
��$\stackrel{��}{b}$=$\frac{112.3-5��4��5}{90-5��{4}^{2}}$=1.23��$\stackrel{��}{a}$��a=5-1.23��4=0.08��
�����Իع�ֱ�߷�����$\stackrel{��}{y}$=1.23x+0.08��
��2����x=10���꣩ʱ��$\stackrel{��}{y}$=1.23��10+0.08=12.38 ����Ԫ����
������ʹ��10��ʱ��֧���ܷ�����12.38��Ԫ��
���� ���⿼�������Իع�ֱ�߷��̵������ûع鷽�̹���Ԥ������������������Ĺؼ������ù�ʽ��ع鷽�̵�ϵ��������Ҫϸ�ģ�

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
6����֪ԲM��x2+y2-2ay=0��a��0����ֱ��x+y=0�����߶εij�����2����ԲM��ԲN����x-1��2+��y-1��2=1��λ�ù�ϵ�ǣ�������
| A�� | ���� | B�� | �ཻ | C�� | ���� | D�� | ���� |
7����x-1����$\frac{1}{x}$+x��6��չ��ʽ�е�һ����ϵ���ǣ�������
| A�� | 5 | B�� | 14 | C�� | 20 | D�� | 35 |
8��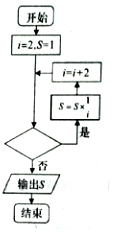 ��ͼ���������Ǽ���������ֵ�ij����ͼ�������жϿ��ڲ������루������
��ͼ���������Ǽ���������ֵ�ij����ͼ�������жϿ��ڲ������루������
 ��ͼ���������Ǽ���������ֵ�ij����ͼ�������жϿ��ڲ������루������
��ͼ���������Ǽ���������ֵ�ij����ͼ�������жϿ��ڲ������루������| A�� | i��2019�� | B�� | i��2019�� | C�� | i��2017�� | D�� | i��2018�� |