题目内容
如图，正方形ABCD内接于椭圆
＝1(a＞b＞0)，且它的四条边与坐标轴平行，正方形MNPQ的顶点M、N在椭圆上，顶点P、Q在正方形的边AB上，且A、M都在第一象限．
(1) 若正方形ABCD的边长为4，且与y轴交于E、F两点，正方形MNPQ的边长为2.
① 求证：直线AM与△ABE的外接圆相切；
② 求椭圆的标准方程；
(2) 设椭圆的离心率为e，直线AM的斜率为k，求证：2e2－k是定值．
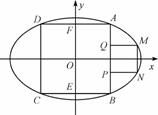
(1) 证明：① 依题意：A(2，2)，M(4，1)，E(0，－2)，∴ 
＝(2，－1)，
＝(－2，－4)，∴ 
＝0，∴ AM⊥AE.
∵ AE为Rt△ABE外接圆直径，∴ 直线AM与△ABE的外接圆相切．
② 解：由
解得椭圆标准方程为
＝1.
(2) 证明：设正方形ABCD的边长为2s，正方形MNPQ的边长为2t，则A(s，s)，M(s＋2t，t)，代入椭圆方程
＝1，
∴ 2e2－k＝2为定值．
练习册系列答案
相关题目
＝1(a>b>0)的焦距为2c，以O为圆心，a为半径的圆．过点
作圆的两切线互相垂直，则离心率e＝________．
＋y2＝1的左右焦点，点P在椭圆上运动．则
的最大值是________．
＝1(a>b>0)，点A、B分别是椭圆C的左顶点和上顶点，直线AB与圆G：
(c是椭圆的半焦距)相离，P是直线AB上一动点，过点P作圆G的两切线，切点分别为M、N.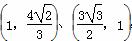
，求椭圆C的方程；
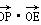的值(O是坐标原点)；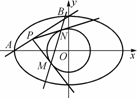
·
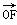＝1.设|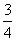
c.若以O为中心，F为一个焦点的椭圆经过点Q，当
取最小值时，求椭圆的方程．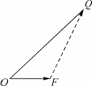
＝1(a>0，b>0)的两条渐近线方程为y＝±
x，若顶点到渐近线的距离为1，求双曲线方程．