题目内容
已知椭圆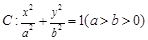
,顺次连结椭圆
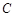的四个顶点,所得四边形的内切圆与长轴的两交点正好是长轴的两个三等分点,则椭圆的离心率
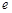等于( ).
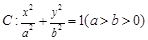,顺次连结椭圆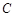的四个顶点,所得四边形的内切圆与长轴的两交点正好是长轴的两个三等分点,则椭圆的离心率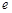等于( ).A． | B． | C． | D． |
B
由椭圆的性质得四边形的内切圆的半径
练习册系列答案
相关题目
题目内容
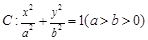,顺次连结椭圆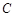的四个顶点,所得四边形的内切圆与长轴的两交点正好是长轴的两个三等分点,则椭圆的离心率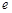等于( ).| A． | B． | C． | D． |
：
的左、右顶点分别为
，
，
为短轴的端点，△
的面积为
，离心率是
．
是椭圆
，
与直线
分别交于
，
两点，证明：以
为直径的圆与直线
相切于点
(
:
的两个焦点为
,点
在椭圆
.
过圆
的圆心，交椭圆
两点，且
对称，求直线
＋
＝1的离心率为( )
的焦点，离心率是
为常数？若存在，求出点M的坐标；若不存在，请说明理由.
的右焦点到直线
的距离是
轴上，一个顶点为
，且其右焦点到直线
的距离为3．
，且过定点
的直线
，使
、
，且
？若存在，求出直线
的离心率为
，直线
:
与以原点为圆心、以椭圆
的短半轴长为半径的圆相切.
，右焦点
，直线
过点
垂
，线段
垂直平分线交
，求点
的方程；
轴上时，在曲线
在横坐标为
的点处的切线为L，则点（3,2）到L的距离是
