题目内容
.(本小题满分12分)已知椭圆的中心在原点,焦点在 轴上,一个顶点为
轴上,一个顶点为 ,且其右焦点到直线
,且其右焦点到直线 的距离为3.
的距离为3.
(1)求椭圆的方程;
(2)是否存在斜率为 ,且过定点
,且过定点 的直线
的直线 ,使
,使 与椭圆交于两个不同的点
与椭圆交于两个不同的点 、
、 ,且
,且 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
 轴上,一个顶点为
轴上,一个顶点为 ,且其右焦点到直线
,且其右焦点到直线 的距离为3.
的距离为3.(1)求椭圆的方程;
(2)是否存在斜率为
 ,且过定点
,且过定点 的直线
的直线 ,使
,使 与椭圆交于两个不同的点
与椭圆交于两个不同的点 、
、 ,且
,且 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.(Ⅰ) . (Ⅱ)
. (Ⅱ) 或
或 。
。
 . (Ⅱ)
. (Ⅱ) 或
或 。
。本试题主要是考查了椭圆方程的求解和直线与椭圆的位置关系的运用。
(1)设椭圆的方程为 ,由已知得
,由已知得 .
.
设右焦点为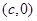 ,由题意得
,由题意得  得到结论。
得到结论。
(2)直线 的方程
的方程 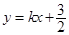 , 代入椭圆方程,得
, 代入椭圆方程,得
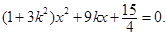
由 得
得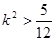 结合韦达定理和
结合韦达定理和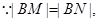
 点
点 在线段
在线段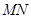 的中垂线上,得到k的值。
的中垂线上,得到k的值。
解:(Ⅰ)设椭圆的方程为 ,由已知得
,由已知得 .
.
设右焦点为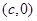 ,由题意得
,由题意得  ……………………………2分
……………………………2分
 .
.
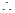 椭圆的方程为
椭圆的方程为 . ……………………4分
. ……………………4分
(Ⅱ)直线 的方程
的方程 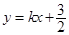 , 代入椭圆方程,得
, 代入椭圆方程,得
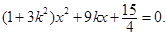
由 得
得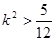 …………………6分
…………………6分
设点 则
则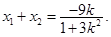
设 、
、 的中点为
的中点为 ,则点
,则点 的坐标为
的坐标为 . ………………8分
. ………………8分
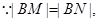
 点
点 在线段
在线段 的中垂线上.
的中垂线上.
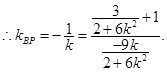 化简,得
化简,得  . ……………………………10分
. ……………………………10分

所以,存在直线 满足题意,直线
满足题意,直线 的方程为
的方程为
 或
或 ……………………………12分
……………………………12分
(1)设椭圆的方程为
 ,由已知得
,由已知得 .
. 设右焦点为
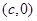 ,由题意得
,由题意得  得到结论。
得到结论。(2)直线
 的方程
的方程 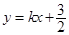 , 代入椭圆方程,得
, 代入椭圆方程,得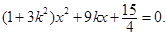
由
 得
得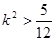 结合韦达定理和
结合韦达定理和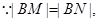
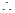 点
点 在线段
在线段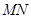 的中垂线上,得到k的值。
的中垂线上,得到k的值。解:(Ⅰ)设椭圆的方程为
 ,由已知得
,由已知得 .
. 设右焦点为
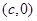 ,由题意得
,由题意得  ……………………………2分
……………………………2分  .
.  椭圆的方程为
椭圆的方程为 . ……………………4分
. ……………………4分 (Ⅱ)直线
 的方程
的方程 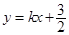 , 代入椭圆方程,得
, 代入椭圆方程,得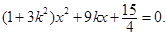
由
 得
得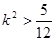 …………………6分
…………………6分设点
 则
则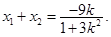
设
 、
、 的中点为
的中点为 ,则点
,则点 的坐标为
的坐标为 . ………………8分
. ………………8分 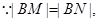
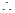 点
点 在线段
在线段 的中垂线上.
的中垂线上. 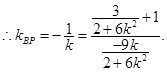 化简,得
化简,得  . ……………………………10分
. ……………………………10分 
所以,存在直线
 满足题意,直线
满足题意,直线 的方程为
的方程为  或
或 ……………………………12分
……………………………12分 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
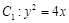 的焦点到准线的距离与椭圆
的焦点到准线的距离与椭圆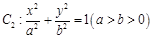 的长半轴相等,设椭圆的右顶点为
的长半轴相等,设椭圆的右顶点为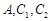 在第一象限的交点为
在第一象限的交点为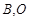 为坐标原点,且
为坐标原点,且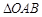 的面积为
的面积为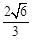
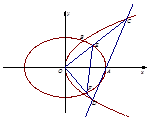
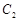 的标准方程;
的标准方程;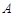 作直线
作直线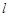 交
交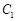 于
于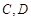 两点,射线
两点,射线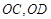 分别交
分别交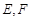 两点.
两点.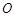 点在以
点在以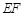 为直径的圆的内部;
为直径的圆的内部;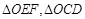 的面积分别为
的面积分别为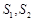 ,问是否存在直线
,问是否存在直线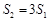 ?请说明理由.
?请说明理由. ,点
,点 是圆内异于
是圆内异于 是圆周上一点.把纸片折叠使点
是圆周上一点.把纸片折叠使点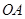 交于
交于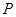 点.当点
点.当点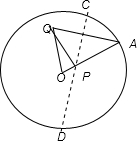
 在
在 轴的非负半轴上,点
轴的非负半轴上,点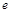 ;
; 为焦点
为焦点 的对称点,动点
的对称点,动点 满足
满足 ,问是否存在一个定点
,问是否存在一个定点 ,使
,使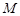 是椭圆
是椭圆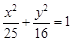 上的一点,
上的一点,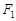 、
、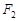 为焦点,
为焦点,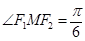 ,则
,则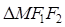
 ( )
( )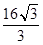
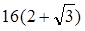
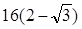
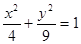 于A、B两点,且M为AB的中点,则直线l方程为 .
于A、B两点,且M为AB的中点,则直线l方程为 . (a>b>0)的左右焦点分别为F1,F2,P是椭圆上一点。
(a>b>0)的左右焦点分别为F1,F2,P是椭圆上一点。 PF1F2为以F2P为底边的等腰三角形,当60°<
PF1F2为以F2P为底边的等腰三角形,当60°< PF1F2
PF1F2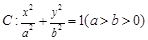 ,顺次连结椭圆
,顺次连结椭圆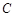 的四个顶点,所得四边形的内切圆与长轴的两交点正好是长轴的两个三等分点,则椭圆的离心率
的四个顶点,所得四边形的内切圆与长轴的两交点正好是长轴的两个三等分点,则椭圆的离心率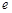 等于( ).
等于( ).



 (
(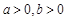 )的一条渐近线方程为
)的一条渐近线方程为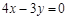 ,则该双曲
,则该双曲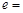 _________.
_________.