题目内容
19.已知a1=1,an+1=${a}_{n}{+2}^{n}$,求通项公式an.分析 当n≥2时,利用an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1计算即得结论.
解答 解:当n≥2时,an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
=2n-1+2n-2+…+2+1
=$\frac{1-{2}^{n}}{1-2}$
=2n-1,
又∵a1=1满足上式,
∴an=2n-1.
点评 本题考查数列的通项公式,考查运算求解能力,注意解题方法的积累,属于基础题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
9.阅读如图的程序框图,当该程序运行后输出的S值是( )
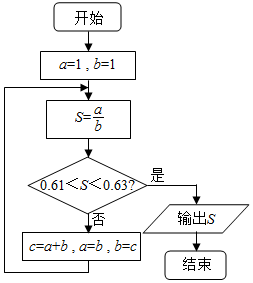

| A. | $\frac{3}{5}$ | B. | $\frac{5}{8}$ | C. | $\frac{8}{13}$ | D. | $\frac{13}{21}$ |
10.下列命题中是全称命题,并且又是真命题的是( )
| A. | 所有菱形的四条边都相等 | B. | ?x0∈N,使2x0为偶数 | ||
| C. | 对?x∈R,x2+2x+1>0 | D. | π是无理数 |
7.数列{an}是递增数列,且满足an+1=f(an),a1∈(0,1),则f(x)不可能是( )
| A. | f(x)=$\sqrt{x}$ | B. | f(x)=2x-1 | C. | f(x)=$\sqrt{2x-{x}^{2}}$ | D. | f(x)=log2(x+1) |
1.抛物线y2=4x的动点AB的长为6,则AB的中点M到y轴的最短距离是( )
| A. | 3 | B. | 1 | C. | 2 | D. | 4 |