题目内容
已知圆x2+y2=r2在曲线|x|+|y|=4的内部，则半径r的范围是（ ）
| A、0＜r＜2 | ||
B、0＜r＜
| ||
C、0＜r＜2
| ||
| D、0＜r＜4 |
考点：点与圆的位置关系
专题：直线与圆
分析：作出曲线|x|+|y|=4对应的图象，利用圆心到直线的距离d与半径之间的关系进行判断即可．
解答：
解：作出曲线|x|+|y|=4对应的图象如图：
但x＞0，y＞0时，曲线对应的方程为x+y-4=0，
若圆x2+y2=r2在曲线|x|+|y|=4的内部，
则圆心到直线的距离d=
＞r，
即r＜2
，
故0＜r＜2
，
故选：C
但x＞0，y＞0时，曲线对应的方程为x+y-4=0，
若圆x2+y2=r2在曲线|x|+|y|=4的内部，
则圆心到直线的距离d=
| |4| | ||
|
即r＜2
| 2 |
故0＜r＜2
| 2 |
故选：C
点评：本题主要考查直线和圆的位置关系的应用，根据点到直线的距离公式是解决本题的关键．
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
半径为2cm的球的体积是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
△ABC中，若cosA+cosB=sinC，则△ABC的形状是（ ）
| A、等腰三角形 |
| B、等边三角形 |
| C、等腰直角三角形 |
| D、直角三角形 |
已知函数f（x）=sin（2x+φ），其中φ为实数，若f（
）=1，则函数g（x）=2cos（2x+φ）+1的单调递增区间是（ ）
| π |
| 3 |
A、[kπ-
| ||||
B、[kπ+
| ||||
C、[kπ-
| ||||
D、[kπ-
|
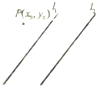如图，点P（x0，y0）到直线l1：Ax+By+C=0，l2：Ax+By+C′=0（C≠C′）的有向距离分别为δ1=| Ax0+By0+C | ||
|
| Ax0+By0+C′ | ||
|
A、0＜
| ||||||
B、-1＜
| ||||||
C、
| ||||||
D、
|