题目内容
求下列函数的导数：
y=2xtanx．
y=2xtanx．
考点：导数的运算
专题：导数的综合应用
分析：直接利用导数的运算法则计算．
解答：
解：∵y=2xtanx，
∴y′=（2xtanx）′=（2x）′tanx+2x•（tanx）′=2tanx+2xsec2x．
∴y′=（2xtanx）′=（2x）′tanx+2x•（tanx）′=2tanx+2xsec2x．
点评：本题考查了基本初等函数的导数公式，是基础的计算题．
练习册系列答案
目标测试系列答案
相关题目
在锐角三角形ABC中，角A，B，C对应的边长分别为a，b，c，若a，b，c成等比数列，则cosB的取值范围是（ ）
A、（0，
| ||||||
B、（0，
| ||||||
C、[
| ||||||
D、[
|
已知i是虚数单位，集合M=N（整数集），集合N=（i，i2，i3，i4），则集合M∩N的元素共有（ ）
| A、3个 | B、2个 | C、1个 | D、无穷个 |
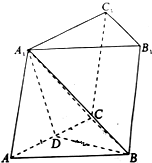如图，在三棱锥ABC-A1B1C1中，△ABC为等边三角形，AB=2，AA1=
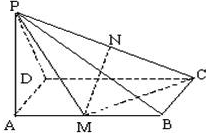如图所示，四棱锥P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，M、N分别是AB、PC的中点，PA=AD=a．