题目内容
 如图,角α(α∈(
如图,角α(α∈(| π |
| 6 |
| π |
| 2 |
| π |
| 4 |
(Ⅰ)若x1=
| 3 |
| 5 |
(Ⅱ)过点A、B分别作x轴的垂线,垂足依次为C、D,记△AOC、△BOD的面积分别为S1、S2,若S1=
| 3 |
考点:正弦定理
专题:三角函数的图像与性质
分析:(Ⅰ)先根据三角函数的定义分别表示出x1,y1和x2,y2,进而根据x1的值求得sinα和cosα的值,最后利用两角和公式求得x2的值;
(Ⅱ)用三角形面积公式分别表示出△AOC、△BOD的面积根据已知关系,求得α的值.
(Ⅱ)用三角形面积公式分别表示出△AOC、△BOD的面积根据已知关系,求得α的值.
解答:
解:如图,由三角函数的定义知:

x1=cosα,y1=sinα,x2=cos(α+
),y2=sin(α+
).
(Ⅰ)∵x1=cosα=
,
∴sinα=
,
∴x2=cos(α+
)=cosαcos
-sinαsin
=
×
-
×
=-
.
(Ⅱ)S1=
|OC|•|AC|=
|cosα•sinα|=
|sin2α|,S2=
|OD|•|BD|=
|cos(α+
)sin(α+
)=
|cos2α|,
∵S1=
S2,
∴|sin2α|=
|cos2α|⇒|tan2α|=
,
∵
<α<
,
∴
<2α<π,
∴2α=
⇒α=
.

x1=cosα,y1=sinα,x2=cos(α+
| π |
| 4 |
| π |
| 4 |
(Ⅰ)∵x1=cosα=
| 3 |
| 5 |
∴sinα=
| 4 |
| 5 |
∴x2=cos(α+
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 3 |
| 5 |
| ||
| 2 |
| 4 |
| 5 |
| ||
| 2 |
| ||
| 10 |
(Ⅱ)S1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 1 |
| 4 |
∵S1=
| 3 |
∴|sin2α|=
| 3 |
| 3 |
∵
| π |
| 6 |
| π |
| 2 |
∴
| π |
| 3 |
∴2α=
| 2π |
| 3 |
| π |
| 3 |
点评:本题主要考查了三角函数的定义和正弦定理的应用.注重了对学生基础知识的考查.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图所示,四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD,∠ABC=45°,AB=SA=SB=2.
如图所示,四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD,∠ABC=45°,AB=SA=SB=2. 已知ABCD是正方形,PA⊥面ABCD,且PA=AB,E,F是侧棱PD,PC的中点.
已知ABCD是正方形,PA⊥面ABCD,且PA=AB,E,F是侧棱PD,PC的中点.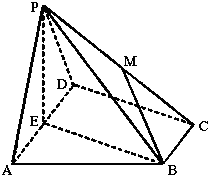 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,E为AD的中点,M是棱PC的中点,PA=PD=2,BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,E为AD的中点,M是棱PC的中点,PA=PD=2,BC=