题目内容
 如图所示,四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD,∠ABC=45°,AB=SA=SB=2.
如图所示,四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD,∠ABC=45°,AB=SA=SB=2.(1)证明:SA⊥BC;
(2)求点B到平面SAD的距离.
考点:点、线、面间的距离计算,直线与平面垂直的性质
专题:平面向量及应用,空间位置关系与距离
分析:(1)作SO⊥BC,垂足为O,连结AO,由侧面SBC⊥底面ABCD,得SO⊥底面ABCD,连接AO.由条件SA=SB,可以说明OA=OB,因为∠ABC=45°,所以OB⊥OA,从而证明BO⊥平面SAO,所以BO⊥平面SAO,所以SA⊥BC.
(2)要求B到平面SAD的距离,需要过B作平面SAD的垂线,垂足为E,这样直接作不好作,所以想着建立空间直角坐标系,用向量解决.可以分别以OA,OB,OS为x轴,y轴,z轴,建立空间直角坐标系,通过BE⊥平面SAD,E在平面SAD上,会得到向量的一些关系,从而求出E点的坐标,再根据两点间的距离公式求出BE.
(2)要求B到平面SAD的距离,需要过B作平面SAD的垂线,垂足为E,这样直接作不好作,所以想着建立空间直角坐标系,用向量解决.可以分别以OA,OB,OS为x轴,y轴,z轴,建立空间直角坐标系,通过BE⊥平面SAD,E在平面SAD上,会得到向量的一些关系,从而求出E点的坐标,再根据两点间的距离公式求出BE.
解答:
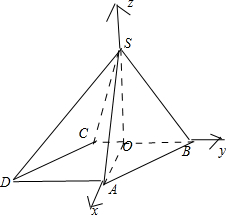 (1)证明:作SO⊥BC,垂足是O,连接AO,SO,
(1)证明:作SO⊥BC,垂足是O,连接AO,SO,
∵侧面SBC⊥底面ABCD,侧面SBC∩底面ABCD=BC
∴SO⊥底面ABCD;
又∵OA?底面ABCD,OB?底面ABCD
∴SO⊥OA,SO⊥OB;
又 SA=SB
∴OA=OB;
又∠ABC=45°
∴OA⊥OB;
∵BC⊥SO,BC⊥AO,SO∩AO=O
∴BC⊥平面SOA;
又∵SA?平面SOA
∴SA⊥BC.
(2)分别以OA,OB,OS为x轴,y轴,z轴建立空间直角坐标系.
在Rt△AOB中,∠,∠ABO=45°,AB=2;
∴OA=OB=
;
在Rt△BOS中,∠SOB=90°,OB=
,SB=2;
∴OS=
.
设D(
,a,0),过B作平面SAD的垂线,垂足为E(x0,y0,z0),并且能确定以下几个点的坐标:
A(
,0,0),S(0,0,
),B(0,
,0);
∴
=(x0-
,y0,z0),
=(0,a,0),
=(-
,0,
),
=(x0,y0-
,z0);
∵
,
,
都在平面SAD上,∴存在实数λ,μ使:
=λ
+μ
;
∴带入坐标可得:
(1)
∵
⊥平面SAD,∴
⊥
,
⊥
;
∴
(2)
由(1)(2)解得:x0=
,y0=
,z0=
;
∴BE=1.
∴点B到平面SAD的距离为:1.
 (1)证明:作SO⊥BC,垂足是O,连接AO,SO,
(1)证明:作SO⊥BC,垂足是O,连接AO,SO,∵侧面SBC⊥底面ABCD,侧面SBC∩底面ABCD=BC
∴SO⊥底面ABCD;
又∵OA?底面ABCD,OB?底面ABCD
∴SO⊥OA,SO⊥OB;
又 SA=SB
∴OA=OB;
又∠ABC=45°
∴OA⊥OB;
∵BC⊥SO,BC⊥AO,SO∩AO=O
∴BC⊥平面SOA;
又∵SA?平面SOA
∴SA⊥BC.
(2)分别以OA,OB,OS为x轴,y轴,z轴建立空间直角坐标系.
在Rt△AOB中,∠,∠ABO=45°,AB=2;
∴OA=OB=
| 2 |
在Rt△BOS中,∠SOB=90°,OB=
| 2 |
∴OS=
| 2 |
设D(
| 2 |
A(
| 2 |
| 2 |
| 2 |
∴
| AE |
| 2 |
| AD |
| AS |
| 2 |
| 2 |
| BE |
| 2 |
∵
| AE |
| AD |
| AS |
| AE |
| AD |
| AS |
∴带入坐标可得:
|
∵
| BE |
| BE |
| AS |
| BE |
| AD |
∴
|
由(1)(2)解得:x0=
| ||
| 2 |
| 2 |
| ||
| 2 |
∴BE=1.
∴点B到平面SAD的距离为:1.
点评:本题考查的知识点是:面面垂直的性质定理,线面垂直判定定理,线线垂直的判定方法,线面垂直的性质,空间直角坐标系,共面向量基本定理,相互垂直的向量的数量积为0,要掌握这种用向量的办法求点到平面的距离的求法.

练习册系列答案
相关题目
 如图,角α(α∈(
如图,角α(α∈(