题目内容
5.若实数x,y满足$\left\{\begin{array}{l}x+y-4≤0\\ 2x-y-4≤0\\ x-y+2≥0\end{array}\right.$,则目标函数z=2x+3y的最大值为( )| A. | 11 | B. | 24 | C. | 36 | D. | 49 |
分析 作出不等式组对应的平面区域,利用z的几何意义,利用数形结合即可得到结论.
解答  解:作出不等式组$\left\{\begin{array}{l}x+y-4≤0\\ 2x-y-4≤0\\ x-y+2≥0\end{array}\right.$对应的平面区域如图
解:作出不等式组$\left\{\begin{array}{l}x+y-4≤0\\ 2x-y-4≤0\\ x-y+2≥0\end{array}\right.$对应的平面区域如图
由z=2x+3y得y=-$\frac{2}{3}$x+$\frac{z}{3}$,
平移直线y=-$\frac{2}{3}$x+$\frac{z}{3}$,
由图象可知当直线y=-$\frac{2}{3}$x+$\frac{z}{3}$,
经过点A时,
直线y=-$\frac{2}{3}$x+$\frac{z}{3}$,
的截距最大,此时z最大,
由$\left\{\begin{array}{l}x+y-4=0\\ x-y+2=0\end{array}\right.$,解得$\left\{\begin{array}{l}x=1\\ y=3\end{array}\right.$,
即A(1,3),
此时z=2×1+3×3=11,
故选:A.
点评 本题主要考查线性规划的应用,利用z的几何意义,通过数形结合是解决本题的关键.

练习册系列答案
相关题目
16.不等式(x+5)(3-2x)≥6的解集是( )
| A. | {x|-$\frac{9}{2}$≤x≤1} | B. | {x|-1≤x≤$\frac{9}{2}$} | C. | {x|x≤-$\frac{9}{2}$或x≥1} | D. | {x|x≤-1或x≥$\frac{9}{2}$} |
13.已知a,b∈R,那么“a2>b2”是“a>|b|”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充分必要条件 | D. | 既非充分又非必要条件 |
20.函数$f(x)=-\frac{1}{1+x}$在x∈[1,+∞)上的值域为( )
| A. | $({-∞,-\frac{1}{2}}]$ | B. | $[{-\frac{1}{2},+∞})$ | C. | $[{-\frac{1}{2},0})$ | D. | $[-\frac{1}{2},0]$ |
17.若$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$是同一个平面α内的两个向量,则( )
| A. | 平面α内任一向量$\overrightarrow{a}$,都有$\overrightarrow{a}$=λ$\overrightarrow{{e}_{1}}$+μ$\overrightarrow{{e}_{2}}$(λ,μ∈R) | |
| B. | 若存在实数λ1,λ2,使λ1$\overrightarrow{{e}_{1}}$+λ2$\overrightarrow{{e}_{2}}$=0,则λ1=λ2=0 | |
| C. | 若$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$不共线,则空间任一向量$\overrightarrow{a}$,都有$\overrightarrow{a}$=λ$\overrightarrow{{e}_{1}}$+μ$\overrightarrow{{e}_{2}}$(λ,μ∈R) | |
| D. | 若$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$不共线,则平面任一向量$\overrightarrow{a}$,都有$\overrightarrow{a}$=λ$\overrightarrow{{e}_{1}}$+μ$\overrightarrow{{e}_{2}}$(λ,μ∈R) |
15.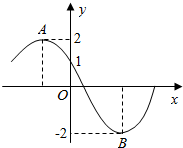 如图为函数f(x)=Msin(ωx+φ)(M>0,ω>0,0≤φ≤π)的部分图象,若点A、B分别为函数f(x)的最高点与最低点,且|AB|=5,那么f(-1)=( )
如图为函数f(x)=Msin(ωx+φ)(M>0,ω>0,0≤φ≤π)的部分图象,若点A、B分别为函数f(x)的最高点与最低点,且|AB|=5,那么f(-1)=( )
 如图为函数f(x)=Msin(ωx+φ)(M>0,ω>0,0≤φ≤π)的部分图象,若点A、B分别为函数f(x)的最高点与最低点,且|AB|=5,那么f(-1)=( )
如图为函数f(x)=Msin(ωx+φ)(M>0,ω>0,0≤φ≤π)的部分图象,若点A、B分别为函数f(x)的最高点与最低点,且|AB|=5,那么f(-1)=( )| A. | 2 | B. | $\sqrt{3}$ | C. | -$\sqrt{3}$ | D. | -2 |
 某赛季甲,乙两名篮球运动员每场比赛得分可用茎叶图表示如下:
某赛季甲,乙两名篮球运动员每场比赛得分可用茎叶图表示如下: