题目内容
20.函数f(x)=sinx-lg|x|的零点个数( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
分析 求函数y=lg|x|的图象和函数y=sinx的图象的交点个数,数形结合可得结论.
解答  解:令f(x)=0,
解:令f(x)=0,
∴lg|x|=sinx,
令g(x)=lg|x|,h(x)=sinx,
∴将函数f(x)的零点个数问题转化为
g(x),h(x)的交点个数问题,
画出g(x),h(x)的图象,
如图所示:共6个交点,
故选:B.
点评 本题主要考查函数的两点个数的判断方法,体现了转化以及数形结合的数学思想,属于中档题.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
8.已知一个几何体的三视图如图所示,若该几何体的体积为$\frac{10}{3}$,则a+b2的最小值为( )
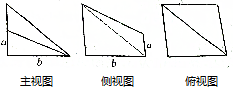

| A. | 4$\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | 4 | D. | 4$\sqrt{2}$ |
15.已知向量$\overrightarrow a$,$\overrightarrow b$的夹角为60°,且|$\overrightarrow a$|=1,|$\overrightarrow{b}$|=2,则|2$\overrightarrow a$+$\overrightarrow{b}$|=( )
| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $2\sqrt{2}$ | D. | $2\sqrt{3}$ |
5.0到9之间取整数值的随机数,指定0,1表示没有击中目标,2,3,4,5,6,7,8,9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了20组随机数:
7527 0293 7140 9857 0347 4373 8636 6947 1417 4698
0371 6233 2616 8045 6011 3661 9597 7424 7610 4281
根据以上数据估计该射击运动员射击4次至少击中3次的概率为( )
7527 0293 7140 9857 0347 4373 8636 6947 1417 4698
0371 6233 2616 8045 6011 3661 9597 7424 7610 4281
根据以上数据估计该射击运动员射击4次至少击中3次的概率为( )
| A. | 0.852 | B. | 0.8192 | C. | 0.8 | D. | 0.75 |
7.清华大学自主招生考试题中要求考生从A,B,C三道题中任选一题作答,考试结束后,统计数据显示共有600名学生参加测试,选择A,B,C三题答卷数如下表:
(Ⅰ)负责招生的教授为了解参加测试的学生答卷情况,现用分层抽样的方法从600份答案中抽出若干份答卷,其中从选择A题作答的答卷中抽出了3份,则应分别从选择B,C题作答的答卷中各抽出多少份?
(Ⅱ)测试后的统计数据显示,A题的答卷得优的有60份,若以频率作为概率,在(Ⅰ)问中被抽出的选择A题作答的答卷中,记其中得优的份数为X,求X的分布列及其数学期望E(X).
| 题 | A | B | C |
| 答卷数 | 180 | 300 | 120 |
(Ⅱ)测试后的统计数据显示,A题的答卷得优的有60份,若以频率作为概率,在(Ⅰ)问中被抽出的选择A题作答的答卷中,记其中得优的份数为X,求X的分布列及其数学期望E(X).
 的图象可能是( )
的图象可能是( )
 等于( )
等于( )