题目内容
15.已知向量$\overrightarrow a$,$\overrightarrow b$的夹角为60°,且|$\overrightarrow a$|=1,|$\overrightarrow{b}$|=2,则|2$\overrightarrow a$+$\overrightarrow{b}$|=( )| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $2\sqrt{2}$ | D. | $2\sqrt{3}$ |
分析 由题意可得,$\overrightarrow{a}•\overrightarrow{b}$=1×2×cos60°=1,再根据|2$\overrightarrow a$+$\overrightarrow{b}$|=$\sqrt{{(2\overrightarrow{a}+\overrightarrow{b})}^{2}}$,计算求的结果.
解答 解:∵向量$\overrightarrow a$,$\overrightarrow b$的夹角为60°,且|$\overrightarrow a$|=1,|$\overrightarrow{b}$|=2,∴$\overrightarrow{a}•\overrightarrow{b}$=1×2×cos60°=1,
∴|2$\overrightarrow a$+$\overrightarrow{b}$|=$\sqrt{{(2\overrightarrow{a}+\overrightarrow{b})}^{2}}$=$\sqrt{{4\overrightarrow{a}}^{2}+4\overrightarrow{a}•\overrightarrow{b}{+\overrightarrow{b}}^{2}}$=$\sqrt{4+4+4}$=2$\sqrt{3}$,
故选:D.
点评 本题主要考查两个向量的数量积的定义,求向量的模的方法,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.函数f(x)=sinx-lg|x|的零点个数( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
7.国务院总理李克强在2015年4月14日的经济形势座谈会上就“手机流量资费和网速”问题做出重要指示,工信部回应,将加大今年宽带专项行动中“加快4G建设”、“大幅提升网速”等重点工作的推进力度,为此某移动部门对部分4G手机用户每日使用流量(单位:M)进行统计,得到如下记录:
将手机日使用流量统计到各组的频率视为概率,并假设每天手机日使用流量相互独立.
(Ⅰ)求某人在未来连续4天里,有连续3天的手机日使用流量都不低于15M,且另1天的手机日使用流量低于5M的概率;
(Ⅱ)用X表示某人在未来3天时间里手机日使用流量不低于15M的天数,求X的分布列和期望.
| 流量(x) | 0≤x<5 | 5≤x<10 | 10≤x<15 | 15≤x<20 | 20≤x<25 | x≥25 |
| 频率 | 0.05 | 0.25 | 0.30 | 0.25 | 0.15 | 0 |
(Ⅰ)求某人在未来连续4天里,有连续3天的手机日使用流量都不低于15M,且另1天的手机日使用流量低于5M的概率;
(Ⅱ)用X表示某人在未来3天时间里手机日使用流量不低于15M的天数,求X的分布列和期望.
3.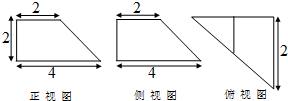 已知某几何体的三视图如图所示,其中正视图和侧视图为全等的直角梯形,俯视图为直角三角形则该几何体的表面积为( )
已知某几何体的三视图如图所示,其中正视图和侧视图为全等的直角梯形,俯视图为直角三角形则该几何体的表面积为( )
 已知某几何体的三视图如图所示,其中正视图和侧视图为全等的直角梯形,俯视图为直角三角形则该几何体的表面积为( )
已知某几何体的三视图如图所示,其中正视图和侧视图为全等的直角梯形,俯视图为直角三角形则该几何体的表面积为( )| A. | 6+12$\sqrt{2}$ | B. | 16+12$\sqrt{2}$ | C. | 6+12$\sqrt{3}$ | D. | 16+12$\sqrt{3}$ |
 ,
, ,若实数
,若实数 分别是
分别是 的零点,则( )
的零点,则( ) B.
B.
 D.
D.
 为锐角,且
为锐角,且 ,则
,则 .
.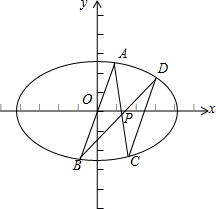 如图,在平面直角坐标系xOy中,已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,点A($\frac{1}{3}$,$\frac{2}{3}$)在椭圆E上,射线AO与椭圆E的另一交点为B,点P(-4t,t)在椭圆E内部,射线AP、BP与椭圆E的另一交点分别为C,D.
如图,在平面直角坐标系xOy中,已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,点A($\frac{1}{3}$,$\frac{2}{3}$)在椭圆E上,射线AO与椭圆E的另一交点为B,点P(-4t,t)在椭圆E内部,射线AP、BP与椭圆E的另一交点分别为C,D.