题目内容
12.在△ABC中,|AB|=1,|AC|=$\sqrt{3}$,若|$\overrightarrow{AB}$+$\overrightarrow{AC}$|=|$\overrightarrow{BC}$|,则其形状为③;若?λ∈R使|λ$\overrightarrow{AB}$-$\overrightarrow{AC}$|≤$\sqrt{2}$成立,则$\overrightarrow{AB}$•$\overrightarrow{AC}$的范围是$(-\sqrt{3},-1]∪[1,\sqrt{3})$(①锐角三角形 ②钝角三角形 ③直角三角形,在横线上填上序号).
分析 (1)利用|$\overrightarrow{AB}$+$\overrightarrow{AC}$|=|$\overrightarrow{BC}$|和$\overrightarrow{AC}$-$\overrightarrow{AB}$=$\overrightarrow{BC}$,两边平方得出$\overrightarrow{AB}$•$\overrightarrow{AC}$=0,$\overrightarrow{AB}$⊥$\overrightarrow{AC}$即可;
(2)利用|λ$\overrightarrow{AB}$-$\overrightarrow{AC}$|≤$\sqrt{2}$平方后λ2-2λ$\overrightarrow{AB}$•$\overrightarrow{AC}$+1≤0有实数解,△≥0,得出$\overrightarrow{AB}$•$\overrightarrow{AC}$≤-1或$\overrightarrow{AB}$•$\overrightarrow{AC}$≥1;
再由-|$\overrightarrow{AB}$|×|$\overrightarrow{AC}$|<$\overrightarrow{AB}$•$\overrightarrow{AC}$<|$\overrightarrow{AB}$|×|$\overrightarrow{AC}$|,即可得出$\overrightarrow{AB}$•$\overrightarrow{AC}$的取值范围.
解答 解:(1)△ABC中,|$\overrightarrow{AB}$+$\overrightarrow{AC}$|=|$\overrightarrow{BC}$|,
∴${\overrightarrow{AB}}^{2}$+${\overrightarrow{AC}}^{2}$+2$\overrightarrow{AB}$•$\overrightarrow{AC}$=${\overrightarrow{BC}}^{2}$;
$\overrightarrow{AC}$-$\overrightarrow{AB}$=$\overrightarrow{BC}$,
∴${\overrightarrow{AC}}^{2}$+${\overrightarrow{AB}}^{2}$-2$\overrightarrow{AB}$•$\overrightarrow{AC}$=${\overrightarrow{BC}}^{2}$;
∴$\overrightarrow{AB}$•$\overrightarrow{AC}$=0
∴$\overrightarrow{AB}$⊥$\overrightarrow{AC}$,
∴△ABC是直角三角形;
(2)?λ∈R,使|λ$\overrightarrow{AB}$-$\overrightarrow{AC}$|≤$\sqrt{2}$成立,
∴λ2${\overrightarrow{AB}}^{2}$-2λ$\overrightarrow{AB}$•$\overrightarrow{AC}$+${\overrightarrow{AC}}^{2}$≤2,
即λ2-2λ$\overrightarrow{AB}$•$\overrightarrow{AC}$+1≤0有实数解,
∴△=4${(\overrightarrow{AB}•\overrightarrow{AC})}^{2}$-4≥0,
解得$\overrightarrow{AB}$•$\overrightarrow{AC}$≤-1或$\overrightarrow{AB}$•$\overrightarrow{AC}$≥1;
又△ABC中,|AB|=1,|AC|=$\sqrt{3}$,
∴-1×$\sqrt{3}$=-|$\overrightarrow{AB}$|×|$\overrightarrow{AC}$|<$\overrightarrow{AB}$•$\overrightarrow{AC}$<|$\overrightarrow{AB}$|×|$\overrightarrow{AC}$|=1×$\sqrt{3}$;
∴$\overrightarrow{AB}$•$\overrightarrow{AC}$的取值范围是(-$\sqrt{3}$,-1]∪[1,$\sqrt{3}$).
故答案为:③,$(-\sqrt{3},-1]∪[1,\sqrt{3})$.
点评 本题考查了平面向量的线性运算与数量积的应用问题,是综合性题目.

| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
| 流量(x) | 0≤x<5 | 5≤x<10 | 10≤x<15 | 15≤x<20 | 20≤x<25 | x≥25 |
| 频率 | 0.05 | 0.25 | 0.30 | 0.25 | 0.15 | 0 |
(Ⅰ)求某人在未来连续4天里,有连续3天的手机日使用流量都不低于15M,且另1天的手机日使用流量低于5M的概率;
(Ⅱ)用X表示某人在未来3天时间里手机日使用流量不低于15M的天数,求X的分布列和期望.
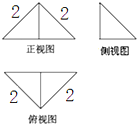 把边长为2的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的三视图如图所示,则这个三棱锥的表面积为( )
把边长为2的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的三视图如图所示,则这个三棱锥的表面积为( )| A. | 2$\sqrt{3}$+4 | B. | 4$\sqrt{3}$ | C. | 8 | D. | 2$\sqrt{3}$+2 |
 标记.
标记.