题目内容
8.已知一个几何体的三视图如图所示,若该几何体的体积为$\frac{10}{3}$,则a+b2的最小值为( )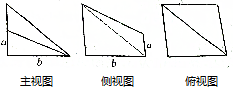
| A. | 4$\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | 4 | D. | 4$\sqrt{2}$ |
分析 由已知的三视图可得几何体的直观图,进而根据该几何体的体积为$\frac{10}{3}$,结合基本不等式可得a+b2的最小值.
解答 解:由已知的三视图可得该几何体的直观图如下所示:
它是由三棱柱ABC-DEF切去一个三棱锥F-ADG所得的组合体,
故体积V=$\frac{1}{2}$×2ab×b-$\frac{1}{3}$×$\frac{1}{2}$(2a-a)b×b=$\frac{5}{6}$ab2=$\frac{10}{3}$,
∴ab2=4,
∴a+b2≥2$\sqrt{a{b}^{2}}$=4,
∴a+b2的最小值为4,
故选:C.
点评 本题考查的知识点是由三视图求体积,考查基本不等式的运用,解决本题的关键是得到该几何体的形状,是基础题.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目
13.曲线y=$\sqrt{1-(x-1)^{2}}$与x轴所围成的区域的面积为( )
| A. | π | B. | $\frac{π}{2}$ | C. | $\frac{3π}{8}$ | D. | $\frac{π}{16}$ |
20.函数f(x)=sinx-lg|x|的零点个数( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
 .
. 的极值;
的极值; ,当
,当 时,
时, 在区间
在区间 内存在极值,求整数
内存在极值,求整数 的值.
的值.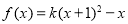 ,
,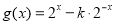 (
(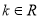 且
且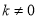 ).
).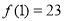 ,求函数
,求函数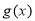 在区间
在区间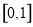 上的值域;
上的值域;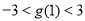 时,函数
时,函数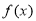 在区间
在区间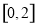 上的最小值大于
上的最小值大于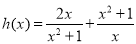 在
在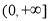 上的最小值,求实数
上的最小值,求实数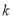 的取值范围.
的取值范围.
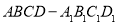 中,
中, 与
与 异面
异面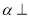 平面
平面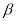 ,平面
,平面 平面
平面 ,则平面
,则平面 平面
平面