题目内容
5.设函数f(x)=$\frac{1}{3}$x3+x2+ax,a∈R,若f(x)在区间(-∞,-$\frac{3}{2}$)单调递增,求a的取值范围.分析 先将问题等价为:f'(x)≥0在x∈(-∞,-$\frac{3}{2}$)上恒成立,再通过分离参数发求a的取值范围.
解答 解:根据题意,问题等价为:
f'(x)≥0在x∈(-∞,-$\frac{3}{2}$)上恒成立,
即x2+2x+a≥0恒成立,
分离参数a得,a≥-x2-2x=-(x+1)2+1,
所以,a≥[-(x+1)2+1]max=$\frac{3}{4}$,
仅当x=-$\frac{3}{2}$时,上式取得最大值,
所以,实数a的取值范围为:[$\frac{3}{4}$,+∞).
点评 本题主要考查了运用导数研究函数的单调性和确定函数的单调区间,涉及不等式恒成立问题的解法,属于基础题.

练习册系列答案
相关题目
10.为了整顿道路交通秩序,某地考虑将对行人闯红灯进行处罚.为了了解市民的态度,在普通行人中随机选取了200人进行调查,当不处罚时,有80人会闯红灯,处罚时,得到如下数据:
若用表中数据所得频率代替率.
(Ⅰ)当罚金定为10元时,行人闯红灯的概率会比不进行处罚降低多少?
(Ⅱ)将选取的200人中会闯红灯的市民两类:A类市民在罚金不超过10元时就会改正行为;B类是其他市民.现对A类与B类市民按分层抽样的方法抽取4人依次进行深度问卷,则前两位均为B类市民的概率是多少?
| 处罚金额x(单位:元) | 0 | 5 | 10 | 15 | 20 |
| 会闯红灯的人数y | 80 | 50 | 40 | 20 | 10 |
(Ⅰ)当罚金定为10元时,行人闯红灯的概率会比不进行处罚降低多少?
(Ⅱ)将选取的200人中会闯红灯的市民两类:A类市民在罚金不超过10元时就会改正行为;B类是其他市民.现对A类与B类市民按分层抽样的方法抽取4人依次进行深度问卷,则前两位均为B类市民的概率是多少?
3.用数学归纳法证明不等式$\frac{n+2}{2}$<1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+…+$\frac{1}{{2}^{n}}$<n+1(n>1,n∈N*)的过程中,当n=2时,中间式子为( )
| A. | 1 | B. | 1+$\frac{1}{2}$ | C. | 1+$\frac{1}{2}$+$\frac{1}{3}$ | D. | 1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$ |
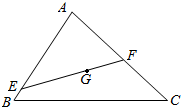 如图,G是△ABC的重心,过G的直线与边AB,AC分别相交于点E,F,若AE=mAB,AF=nAC(mn≠0),求$\frac{1}{m}$+$\frac{1}{n}$的值.
如图,G是△ABC的重心,过G的直线与边AB,AC分别相交于点E,F,若AE=mAB,AF=nAC(mn≠0),求$\frac{1}{m}$+$\frac{1}{n}$的值.