题目内容
13．
某几何体的三视图如图所示，图中的四边形都是边长为4的正方形，两条虚线互相垂直，则该几何体的体积是（ ）| A． | $\frac{176}{3}$ | B． | $\frac{160}{3}$ | C． | $\frac{128}{3}$ | D． | 32 |
分析 由已知中的三视图，可知该几何体是一个正方体的上面挖去了一个底面为正方形，边长为4，高为2的四棱锥．正方体的体积减去挖去的四棱锥，可得该几何体的体积．
解答 解：由已知中的三视图，四边形都是边长为4的正方形，两条虚线互相垂直，可知该几何体是一个正方体的上面挖去了一个底面为正方形，边长为4，高为2的四棱锥．正方体的体积减去挖去的四棱锥，
∴正方体体积V=43=64，
四棱锥$V=\frac{1}{3}×4×4×2$=$\frac{32}{3}$．
那么：该几何体为：64-$\frac{32}{3}$=$\frac{160}{3}$．
故选B
点评 本题主要考查了三视图的投影的认识和体积的计算．属于基础题．
练习册系列答案
相关题目
5．已知函数f（x）是定义在R上的单调函数，且对任意的x，y∈R都有f（x+y）=f（x）+f（y），若动点P（x，y）满足等式f（x2+2x+2）+f（y2+8y+3）=0，则x+y的最大值为（ ）
| A． | 2$\sqrt{6}$-5 | B． | -5 | C． | 2$\sqrt{6}$+5 | D． | 5 |
2．函数$f（x）=cos（ωx+\frac{π}{6}）（ω＞0）$的最小正周期是π，则其图象向右平移$\frac{π}{3}$个单位后的单调递减区间是（ ）
| A． | $[{-\frac{π}{4}+kπ，\frac{π}{4}+kπ}]（k∈Z）$ | B． | $[{\frac{π}{4}+kπ，\frac{3π}{4}+kπ}]（k∈Z）$ | ||
| C． | $[{\frac{π}{12}+kπ，\frac{7π}{12}+kπ}]（k∈Z）$ | D． | $[{-\frac{5π}{12}+kπ，\frac{π}{12}+kπ}]（k∈Z）$ |
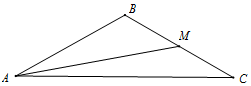如图，在△ABC中，M是边BC的中点，tan∠BAM=$\frac{\sqrt{3}}{5}$，cos∠AMC=-$\frac{2\sqrt{7}}{7}$