题目内容
8.若函数f(x)=ax3+bx2+cx+d(a≠0)图象的对称中心为M(x0,f(x0)),记函数f(x)的导函数为g(x),则有g'(x0)=0.若函数f(x)=x3-3x2,则$f(\frac{1}{2017})+f(\frac{2}{2017})+…+f(\frac{4032}{2017})+f(\frac{4033}{2017})$=-8066.分析 推导出函数f(x)=x3-3x2的对称中心为(1,-2),由此能求出$f(\frac{1}{2017})+f(\frac{2}{2017})+…+f(\frac{4032}{2017})+f(\frac{4033}{2017})$的值.
解答 解:∵f(x)=x3-3x2,∴g(x)=3x2-6x,∴g′(x)=6x-6,
∵g′(x0)=6x0-6=0,∴x0=1,∴f(x0)=f(1)=f(1)=1-3=-2,
∴函数f(x)=x3-3x2的对称中心为(1,-2),
∴f(x)+f(2-x)=-4,
∴$f(\frac{1}{2017})+f(\frac{2}{2017})+…+f(\frac{4032}{2017})+f(\frac{4033}{2017})$=-4×2016+f(1)=-8064+1-3=-8066.
故答案为:-8066.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
19.已知复数z满足z(1+i)=1-i,则|z|=( )
| A. | i | B. | 1 | C. | -i | D. | -1 |
3.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | $\frac{5π}{6}$ | B. | $\frac{4π}{3}$ | C. | $\frac{5π}{3}$ | D. | $\frac{2π}{3}$ |
13. 某几何体的三视图如图所示,图中的四边形都是边长为4的正方形,两条虚线互相垂直,则该几何体的体积是( )
某几何体的三视图如图所示,图中的四边形都是边长为4的正方形,两条虚线互相垂直,则该几何体的体积是( )
 某几何体的三视图如图所示,图中的四边形都是边长为4的正方形,两条虚线互相垂直,则该几何体的体积是( )
某几何体的三视图如图所示,图中的四边形都是边长为4的正方形,两条虚线互相垂直,则该几何体的体积是( )| A. | $\frac{176}{3}$ | B. | $\frac{160}{3}$ | C. | $\frac{128}{3}$ | D. | 32 |
17.设集合A={-1,0,1,2},B={x|x-1<0},则A∩B=( )
| A. | (-1,1) | B. | (-1,0) | C. | {-1,0,1} | D. | {-1,0} |
18.已知函数f(x)=2sin(ωx+φ)(ω>0)的图象与直线y=b(0<b<2)的三个相邻交点的横坐标分别是$\frac{π}{6},\frac{5π}{6},\frac{7π}{6}$,且函数f(x)在x=$\frac{3π}{2}$处取得最小值,那么|φ|的最小值为( )
| A. | $\frac{3π}{2}$ | B. | π | C. | $\frac{π}{2}$ | D. | $\frac{π}{3}$ |
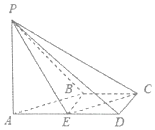 如图,在四棱锥P-ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD=$\frac{1}{2}$AD.E为棱AD的中点,异面直线PA与CD所成的角为90°.
如图,在四棱锥P-ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD=$\frac{1}{2}$AD.E为棱AD的中点,异面直线PA与CD所成的角为90°.