题目内容
已知等式12+22+…+n2=
,以下说法正确的是( )
| 5n2-7n+4 |
| 2 |
| A、仅当n=1时等式成立 |
| B、仅当n=1,2,3时等式成立 |
| C、仅当n=1,2时等式成立 |
| D、n为任何自然数时等式都成立 |
考点:归纳推理
专题:推理和证明
分析:分别令n=1,2,3,4进行检验,得到答案.
解答:
解:当n=1时,左边=1,右边=
=1,成立,当n=2,左边=12+22=5,右边=
=5成立,当n=3,左边=12+22+32=14,右边=
=14成立,
当n=4,左边=12+22+32+42=30,右边=
=28,不成立,
故选:B.
| 5-7+4 |
| 2 |
| 5×22-7×2+4 |
| 2 |
| 5×32-7×3+4 |
| 2 |
当n=4,左边=12+22+32+42=30,右边=
| 5×42-7×4+4 |
| 2 |
故选:B.
点评:本题考查了归纳推理的问题,本题采用的方法是验证,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
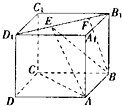 如图正方体ABCD-A1B1C1D1的棱长为2,线段B1D1上有两个动点E、F,且EF=
如图正方体ABCD-A1B1C1D1的棱长为2,线段B1D1上有两个动点E、F,且EF=| 1 |
| 2 |
| A、AC⊥BE |
| B、EF∥平面ABCD |
| C、三棱锥A-BEF的体积为定值 |
| D、△AEF的面积与△BEF的面积相等 |
已知实数x,y满足
,则Z=2x-y的最小值是( )
|
| A、3 | B、-3 | C、5 | D、-5 |
下列函数中,最小正周期为π的是( )
| A、y=|sinx| | ||
| B、y=sinx | ||
C、y=tan
| ||
| D、y=cos4x |
下列有关命题的叙述错误的是( )
| A、对于命题P:?x∈R,x2+x+1<0,则¬P为:?x∈R,x2+x+1≥0 |
| B、若“p且q”为假命题,则p,q均为假命题 |
| C、“x>2”是“x2-3x+2>0”的充分不必要条件 |
| D、命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0” |
已知函数f(x)=sin(ωx+
)(x∈R,ω>0)的最小正周期为π,为了得到函数g(x)=sinωx的图象,只要将y=f(x)的图象( )
| π |
| 4 |
A、向右平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向左平移
|
已知函数y=
,则它的导函数是( )
| x-1 |
A、y′=
| ||||
B、y′=
| ||||
C、y′=
| ||||
D、y′=-
|
有A、B两个口袋,A袋装有4个白球,2个黑球;B袋装有3个白球,4个黑球,从A袋、B袋各取2个球交换之后,则A袋中装有4个白球的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
函数y=log(x-1)(3-x)的定义域是( )
| A、(1,2)∪(3,4) |
| B、[1,2]∪[3,4] |
| C、(1,2)∪(2,3) |
| D、[1,2]∪[2,3] |