题目内容
如图，在四棱锥P-ABCD中，侧面三角形PAD是等边三角形，底面ABCD是直角梯形，且AD∥BC，AD⊥CD，平面PAD⊥底面ABCD，E为AD的中点，M是棱PC上一点，且AD=2BC=4，CD=2| 3 |
（1）试确定点M的位置，使得PE∥平面BDM，并证明；
（2）在（1）的条件下，求三棱锥P-MBD的体积．
考点：棱柱、棱锥、棱台的体积,直线与平面平行的性质
专题：综合题,空间位置关系与距离
分析：（1）点M是PC的中点，利用三角形的中位线，证明MO∥PE，即可证明PE∥平面BDM；
（2）利用VP-MBD=VP-DBC-VM-DBC，即可求三棱锥P-MBD的体积．
（2）利用VP-MBD=VP-DBC-VM-DBC，即可求三棱锥P-MBD的体积．
解答：
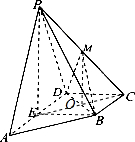解：（1）点M是PC的中点，
连接BE，因为BC∥AD，DE=BC，
所以四边形BCDE为平行四边形
连接EC交BD于O，连接MO，则MO∥PE，
又MO?面BDM，PE?平面BDM，所以PE∥平面BDM．--------------（5分）
（2）由题意VP-MBD=VP-DBC-VM-DBC，
由于平面PAD⊥底面ABCD，三角形PAD是等边三角形，
所以PE⊥AD，所以PE⊥底面ABCD，则PE是三棱锥P-DBC的高，
由题意PA=AD=PD=4，
所以PE=2
，
由（1）知MO是三棱锥M-DBC的高，MO=
，S△DBC=2
，
所以VP-DBC=4，VM-DBC=2，则VP-MBD=2．---------------------（9分）
解：（1）点M是PC的中点，连接BE，因为BC∥AD，DE=BC，
所以四边形BCDE为平行四边形
连接EC交BD于O，连接MO，则MO∥PE，
又MO?面BDM，PE?平面BDM，所以PE∥平面BDM．--------------（5分）
（2）由题意VP-MBD=VP-DBC-VM-DBC，
由于平面PAD⊥底面ABCD，三角形PAD是等边三角形，
所以PE⊥AD，所以PE⊥底面ABCD，则PE是三棱锥P-DBC的高，
由题意PA=AD=PD=4，
所以PE=2
| 3 |
由（1）知MO是三棱锥M-DBC的高，MO=
| 3 |
| 3 |
所以VP-DBC=4，VM-DBC=2，则VP-MBD=2．---------------------（9分）
点评：本题考查线面平行，考查三棱锥的体积，考查学生分析解决问题的能力，属于中档题．．
练习册系列答案
53随堂测系列答案
相关题目
如图，圆M与圆N交于A，B两点，以A为切点作两圆的切线分别交圆M和圆N于C，D两点，延长延长DB交圆M于点E，延长CB交圆N于点F．已知BC=5，DB=10．