题目内容
设f(x)=cosx+
-1.
(Ⅰ)求证:当x≥0时,f(x)≥0;
(Ⅱ)若a∈R,证明:当a≥1时,eax≥sinx-cosx+2对任意的x≥0恒成立.
| x2 |
| 2 |
(Ⅰ)求证:当x≥0时,f(x)≥0;
(Ⅱ)若a∈R,证明:当a≥1时,eax≥sinx-cosx+2对任意的x≥0恒成立.
考点:利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(Ⅰ)由f(x)=cosx+
-1,(x≥0),则f′(x)=x-sinx,设h(x)=x-sinx,则h′(x)=1-cosx,得f′(x)为增函数,从而f(x)在x≥0时为增函数,得f(x)≥f(0)=0;
(Ⅱ)由(Ⅰ)知x≥0时,sinx≤x,cosx≥-
+1,得
+x+1≥sinx-cosx+2,设G(x)=ex-
-x-1,则G′(x)=ex-x-1,设g(x)=ex-x-1,则g′(x)=ex-1,从而G(x)为增函数,进而G(x)≥G(0)=0,即ex≥sinx-cosx+2对任意的x≥0恒成立.又x≥0,a≥1时,eax≥ex,从而a≥1时,eax≥sinx-cosx+2对任意的x≥0恒成立.
| x2 |
| 2 |
(Ⅱ)由(Ⅰ)知x≥0时,sinx≤x,cosx≥-
| x2 |
| 2 |
| x2 |
| 2 |
| x2 |
| 2 |
解答:
(Ⅰ)证明:∵f(x)=cosx+
-1,(x≥0),
则f′(x)=x-sinx,
设h(x)=x-sinx,则h′(x)=1-cosx,
当x≥0时,h′(x)=1-cosx≥0,即f′(x)为增函数,
所以f′(x)≥f′(0)=0,
即f(x)在x≥0时为增函数,
所以f(x)≥f(0)=0;
(Ⅱ)解:由(Ⅰ)知x≥0时,sinx≤x,cosx≥-
+1,
∴
+x+1≥sinx-cosx+2,
设G(x)=ex-
-x-1,则G′(x)=ex-x-1,
设g(x)=ex-x-1,则g′(x)=ex-1,
当x≥0时,g′(x)=ex-1≥0,
∴g(x)=ex-x-1为增函数,
∴g(x)≥g(0)=0,
∴G(x)为增函数,
∴G(x)≥G(0)=0,
∴ex≥sinx-cosx+2对任意的x≥0恒成立.
又x≥0,a≥1时,eax≥ex,
∴a≥1时,eax≥sinx-cosx+2对任意的x≥0恒成立.
| x2 |
| 2 |
则f′(x)=x-sinx,
设h(x)=x-sinx,则h′(x)=1-cosx,
当x≥0时,h′(x)=1-cosx≥0,即f′(x)为增函数,
所以f′(x)≥f′(0)=0,
即f(x)在x≥0时为增函数,
所以f(x)≥f(0)=0;
(Ⅱ)解:由(Ⅰ)知x≥0时,sinx≤x,cosx≥-
| x2 |
| 2 |
∴
| x2 |
| 2 |
设G(x)=ex-
| x2 |
| 2 |
设g(x)=ex-x-1,则g′(x)=ex-1,
当x≥0时,g′(x)=ex-1≥0,
∴g(x)=ex-x-1为增函数,
∴g(x)≥g(0)=0,
∴G(x)为增函数,
∴G(x)≥G(0)=0,
∴ex≥sinx-cosx+2对任意的x≥0恒成立.
又x≥0,a≥1时,eax≥ex,
∴a≥1时,eax≥sinx-cosx+2对任意的x≥0恒成立.
点评:本题考察了函数的单调性,导数的应用,不等式的证明,是一道综合题.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
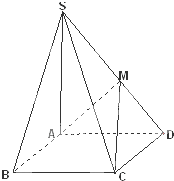 如图,在四棱锥S-ABCD中,底面ABCD为矩形,SA⊥底面ABCD,M为SD的中点,且SA=AD=2AB.
如图,在四棱锥S-ABCD中,底面ABCD为矩形,SA⊥底面ABCD,M为SD的中点,且SA=AD=2AB. 如图,在四棱锥P-ABCD中,侧面三角形PAD是等边三角形,底面ABCD是直角梯形,且AD∥BC,AD⊥CD,平面PAD⊥底面ABCD,E为AD的中点,M是棱PC上一点,且AD=2BC=4,CD=2
如图,在四棱锥P-ABCD中,侧面三角形PAD是等边三角形,底面ABCD是直角梯形,且AD∥BC,AD⊥CD,平面PAD⊥底面ABCD,E为AD的中点,M是棱PC上一点,且AD=2BC=4,CD=2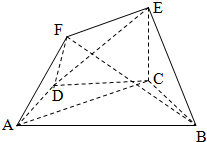 如图,在多面体ABCDEF中,底面ABCD是梯形,且满足AD=DC=CB=
如图,在多面体ABCDEF中,底面ABCD是梯形,且满足AD=DC=CB=