题目内容
2.“2<m<6”是“方程$\frac{{x}^{2}}{m-2}$+$\frac{{y}^{2}}{6-m}$=1为椭圆方程”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 求出方程$\frac{{x}^{2}}{m-2}$+$\frac{{y}^{2}}{6-m}$=1为椭圆方程的充要条件,根据充分必要条件的定义判断即可.
解答 解:若方程$\frac{{x}^{2}}{m-2}$+$\frac{{y}^{2}}{6-m}$=1为椭圆方程,
则$\left\{\begin{array}{l}{m-2>0}\\{6-m>0}\\{m-2≠6-m}\end{array}\right.$,解得:2<m<6,且m≠4,
故“2<m<6”是“方程$\frac{{x}^{2}}{m-2}$+$\frac{{y}^{2}}{6-m}$=1为椭圆方程”的必要不充分条件,
故选:B.
点评 本题考查了充分必要条件,考查椭圆的定义,是一道基础题.

练习册系列答案
相关题目
17.已知幂函数y=f(x)的图象过点$(2\;,\;\;\sqrt{2})$,则$f({\frac{1}{3}})$的值为( )
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{1}{3}$ | C. | 3 | D. | 1 |
14.命题“?x∈R,ex-x-1<0”的否定是( )
| A. | ?x∈R,ex-x-1≥0 | B. | ?x∈R,ex-x-1>0 | C. | ?x∈R,ex-x-1>0 | D. | ?x∈R,ex-x-1≥0 |
11.某工厂甲、乙、丙、丁四个车间生产了同一种产品共计2800件,现要用分层抽样的方法从中抽取140件进行质量检测,且甲、丙两个车间共抽取的产品数量为60,则乙、丁两车间生产的产品总共有( )
| A. | 1000件 | B. | 1200件 | C. | 1400件 | D. | 1600件 |
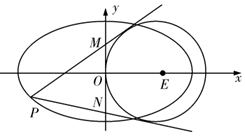 已知椭圆C中心在原点,离心率$\frac{{\sqrt{2}}}{2}$,其右焦点是圆E:(x-1)2+y2=1的圆心.
已知椭圆C中心在原点,离心率$\frac{{\sqrt{2}}}{2}$,其右焦点是圆E:(x-1)2+y2=1的圆心.