题目内容
10.已知Sn为数列{an}的前n项和,若an+1=an-an-1(n∈N*,n≥2),a1=1,a2=3.S2017=1.分析 推导出数列{an}是以6为周期的周期数列,且a1+a2+a3+a4+a5+a6=0,由此能求出S2017=a1=1.
解答 解:因为an+1=an-an-1(n∈N*,n≥2),a1=1,a2=3,
所以a3=a2-a1=2,
a4=a3-a2=-1,
a5=a4-a3=-3,
a6=a5-a4=-2,
a7=a6-a5=1,
所以数列{an}是以6为周期的周期数列,
且a1+a2+a3+a4+a5+a6=0,
故S2017=a1=1.
故答案为:1.
点评 本题考查数列的前2017项和的求法,是基础题,解题时要认真审题,注意数列的周期性的合理运用.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
18.户外运动已经成为一种时尚运动,某单位为了了解员工喜欢户外运动是否与性别有关,对本单位的50名员工进行了问卷调查,得到了如下联表:已知在这50人中随机抽取1人抽到喜欢户外运动的员工的概率是$\frac{3}{5}$
(1)请将列联表补充完整:
(2)是否有99%的把握认为喜欢户外运动与性别有关?并说明理由.下面临界值仅供参考:(大于2.706-90%,大于3.841-95%,大于6.635-99%)
(参考公式:K2=$\frac{{n(ad-bc)}^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
| 喜欢户外活动 | 不喜欢户外活动 | 合计 | |
| 男性 | 20 | 5 | 25 |
| 女性 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
(2)是否有99%的把握认为喜欢户外运动与性别有关?并说明理由.下面临界值仅供参考:(大于2.706-90%,大于3.841-95%,大于6.635-99%)
(参考公式:K2=$\frac{{n(ad-bc)}^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
5.计算 (1+i)(1-i)=( )
| A. | 2i | B. | 1-2i | C. | 2 | D. | 0 |
19.完成下列抽样调查,较为合理的抽样方法依次是( )
①田传利老师从高一年级8名数学老师中抽取一名老师出月考题.
②我校高中三个年级共有2100人,其中高一800人、高二700人、高三600人,白凤库校长为了了解学生对数学的建议,拟抽取一个容量为300的样本;
③我校艺术中心有20排,每排有35个座位,在孟祥锋主任的报告中恰好坐满了同学,报告结束后,为了了解同学意见,学生处需要请20名同学进行座谈.
①田传利老师从高一年级8名数学老师中抽取一名老师出月考题.
②我校高中三个年级共有2100人,其中高一800人、高二700人、高三600人,白凤库校长为了了解学生对数学的建议,拟抽取一个容量为300的样本;
③我校艺术中心有20排,每排有35个座位,在孟祥锋主任的报告中恰好坐满了同学,报告结束后,为了了解同学意见,学生处需要请20名同学进行座谈.
| A. | ①简单随机抽样,②系统抽样,③分层抽样 | |
| B. | ①分层抽样,②系统抽样,③简单随机抽样 | |
| C. | ①系统抽样,②简单随机抽样,③分层抽样 | |
| D. | ①简单随机抽样,②分层抽样,③系统抽样 |
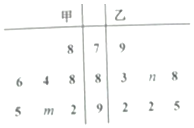 甲、乙两名同学在高一上学期7次物理考试成绩的茎叶图如图所示,其中甲成绩的平均数是88,乙学生的成绩中位数是89,则n-m的值是( )
甲、乙两名同学在高一上学期7次物理考试成绩的茎叶图如图所示,其中甲成绩的平均数是88,乙学生的成绩中位数是89,则n-m的值是( )