题目内容
13.在△ABC中,cos2A+cos2C=2cos2B,求证:$\frac{1}{tanA}$+$\frac{1}{tanC}$=$\frac{2}{tanB}$.分析 将已知移项后,利用和差化积公式化简,整理,利用同角三角函数基本关系式即可证明.
解答 证明:cos2A+cos2C=2cos2B,
⇒cos2A-cos2B=cos2B-cos2C,
⇒2sin(A+B)sin(A-B)=2sin(B+C)sin(B-C),
⇒sinCsin(A-B)=sinAsin(B-C),
⇒sinC(sinAcosB-cosAsinB)=sinA(sinBcosC-cosBsinC),
⇒2sinAcosBsinC=cosAsinBsinC+sinAsinBcosC,(两边同除以sinAsinBsinC)
⇒$\frac{2}{tanB}=\frac{1}{tanA}+\frac{1}{tanC}$.
得证.
点评 本题主要考查了三角函数恒等式的证明,考查了三角函数恒等变换的应用,属于中档题.

练习册系列答案
相关题目
3.已知tanα=$\frac{1}{3}$,则$\frac{sinα-co{s}^{3}α}{sinα+cosα}$=( )
| A. | -$\frac{17}{40}$ | B. | -$\frac{5}{16}$ | C. | -$\frac{34}{45}$ | D. | -$\frac{1}{2}$ |
1.$\frac{{\sqrt{3}-tan{{15}^0}}}{{\sqrt{3}tan{{15}^0}+1}}$=( )
| A. | -1 | B. | $\frac{{\sqrt{3}}}{3}$ | C. | 1 | D. | $\sqrt{3}$ |
8.已知在空间坐标系O-xyz中,点A(-1,2,3)关于平面xOz对称的点的坐标为( )
| A. | (1,2,3) | B. | (-1,-2,3) | C. | (-1,2,-3) | D. | (-1,-2,-3) |
5.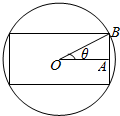 把截面半径为5的圆形木头锯成面积为y的矩形木料,如图,点O为圆心,OA⊥OB,设∠AOB=θ,把面积y表示为θ的表达式,则有( )
把截面半径为5的圆形木头锯成面积为y的矩形木料,如图,点O为圆心,OA⊥OB,设∠AOB=θ,把面积y表示为θ的表达式,则有( )
 把截面半径为5的圆形木头锯成面积为y的矩形木料,如图,点O为圆心,OA⊥OB,设∠AOB=θ,把面积y表示为θ的表达式,则有( )
把截面半径为5的圆形木头锯成面积为y的矩形木料,如图,点O为圆心,OA⊥OB,设∠AOB=θ,把面积y表示为θ的表达式,则有( )| A. | y=50cos2θ | B. | y=25sinθ | C. | y=25sin2θ | D. | y=50sin2θ |
3.某商品进价为每件30元,销售标价为每件50元,若按标价的八折出售,则毛利润为( )
| A. | 20% | B. | 25% | C. | 33.3% | D. | 60% |
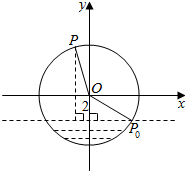 如图,半径为4m的水轮绕着圆心O逆时针做匀速圆周运动,每分钟转动4圈,水轮圆心O距离水面2m,如果当水轮上点P从离开水面的时刻(P0)开始计算时间.
如图,半径为4m的水轮绕着圆心O逆时针做匀速圆周运动,每分钟转动4圈,水轮圆心O距离水面2m,如果当水轮上点P从离开水面的时刻(P0)开始计算时间.


