题目内容
5．
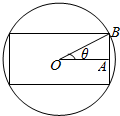把截面半径为5的圆形木头锯成面积为y的矩形木料，如图，点O为圆心，OA⊥OB，设∠AOB=θ，把面积y表示为θ的表达式，则有（ ）| A． | y=50cos2θ | B． | y=25sinθ | C． | y=25sin2θ | D． | y=50sin2θ |
分析 由三角函数可表示矩形的长和宽，由三角函数公式化简可得．
解答 解：由题意可得矩形的长为2OA=2×5cosθ=10cosθ，
矩形的宽为2AB=2×5sinθ=10sinθ，
∴矩形的面积y=10cosθ×10sinθ=50sin2θ
故选：D．
点评 本题考查函数解析式的求解，涉及三角函数化简，属基础题．
练习册系列答案
相关题目
15．若点（1，1）和点（0，2）一个在圆（x-a）2+（y+a）2=4的内部，另一个在圆的外面，则正实数a的取值范围是（ ）
| A． | （1，+∞） | B． | （0，$\frac{1}{2}$） | C． | （0，1） | D． | （1，2） |
16．已知正数x，y满足2x+y+4xy=$\frac{15}{2}$，则2x+y的取值范围为（ ）
| A． | [4，+∞） | B． | [8，+∞） | C． | {6，+∞） | D． | [3，+∞） |
已知函数f（x）是定义在R上的奇函数，当x≥0时，f（x）=2x（1-x）．