题目内容
15.已知一条曲线C在y轴右边,C上每一点到点F(1,0)的距离减去它到y轴距离的差都是1.(1)求曲线C的方程;
(2)过点M(m,0)(m>0)任作一条直线与曲线C交于A,B两点,点N(n,0),连接AN,BN,且m+n=0.求证:∠ANM=∠BNM.
分析 (1)设P(x,y)是曲线C上任意一点,由题意可得C上每一点到点F(1,0)的距离等于它到x=-1的距离,得到x,y的方程,化简即可;
(2)设过点M(m,0)(m>0)的直线l与曲线C的交点为A(x1,y1),B(x2,y2),设l的方程为x=λy+m,代入曲线方程,运用判别式大于0和韦达定理,运用两点的斜率公式计算kAN+kBN,化简整理即可得到所求值.
解答 解:(1)设P(x,y)是曲线C上任意一点,
由题意可得C上每一点到点F(1,0)的距离等于它到x=-1的距离,
那么点P(x,y)满足:$\sqrt{{{(x-1)}^2}+{y^2}}=|{x+1}|$,
化简得y2=4x;
(2)证明:设过点M(m,0)(m>0)的直线l与曲线C的交点为A(x1,y1),B(x2,y2).
设l的方程为x=λy+m,由$\left\{{\begin{array}{l}{x=λy+m}\\{{y^2}=4x}\end{array}}\right.$得y2-4λy-4m=0,△=16(λ2+m)>0,
于是$\left\{{\begin{array}{l}{{y_1}+{y_2}=4λ}\\{{y_1}{y_2}=-4m}\end{array}}\right.$①,
∴kAN+kBN=$\frac{{y}_{1}}{{x}_{1}-n}$+$\frac{{y}_{2}}{{x}_{2}-n}$=$\frac{2λ{y}_{1}{y}_{2}+(m-n)({y}_{1}+{y}_{2})}{({x}_{1}-n)({x}_{2}-n)}$
=$\frac{-8λm+4λ(m-n)}{({x}_{1}-n)({x}_{2}-n)}$=$\frac{-4λ(m+n)}{({x}_{1}-n)({x}_{2}-n)}$,
∵m+n=0,∴kAN+kBN=0,即kAN=-kBN,
则∠ANM=∠BNM.
点评 本题考查抛物线的方程和运用,主要是联立直线和抛物线方程,运用判别式大于0,韦达定理,考查两角相等的证明,注意运用直线的斜率相等,考查化简整理的运算能力,属于中档题.

| A. | (-∞,2] | B. | $({0,\frac{1}{2}}]$ | C. | $[{\frac{1}{2},2}]$ | D. | (0,2] |
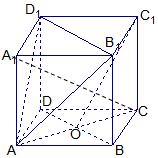 已知正方体ABCD-A1B1C1D1,O是底ABCD对角线的交点.求证:
已知正方体ABCD-A1B1C1D1,O是底ABCD对角线的交点.求证: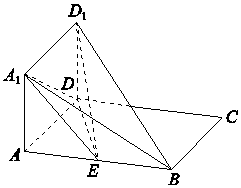 如图所示,四边形ABCD和四边形ADD1A1均为矩形且所在的平面互相垂直,E为线段AB的中点.
如图所示,四边形ABCD和四边形ADD1A1均为矩形且所在的平面互相垂直,E为线段AB的中点.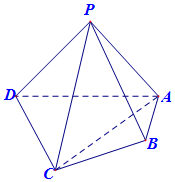 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=$\sqrt{5}$.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=$\sqrt{5}$.