题目内容
若(3x-1)2015=a0+a1x+…+a2015x2015(x∈R),记S2015=
,则S2015的值为 .
| 2015 |
 |
| i=1 |
| ai |
| 3i |
考点:二项式定理的应用,数列的求和
专题:计算题,二项式定理
分析:由(3x-1)2015=a0+a1x+…+a2015x2015(x∈R),得展开式的每一项的系数ar,代入到S2015=
求值即可.
| 2015 |
 |
| i=1 |
| ai |
| 3i |
解答:
解:由题意得:ar=C2015r(-1)2015-r•3r,
∴S2015=
=C20151-C20152+C20153-…-C20152014+C20152015
∵C20150-C20151+C20152-C20153+…+C20152014-C20152015=(1-1)2015=0
∴S2015=1.
故答案为:1.
∴S2015=
| 2015 |
 |
| i=1 |
| ai |
| 3i |
∵C20150-C20151+C20152-C20153+…+C20152014-C20152015=(1-1)2015=0
∴S2015=1.
故答案为:1.
点评:此题考查了二项展开式定理的展开使用及灵活变形求值,特别是解决二项式的系数问题时,常采取赋值法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
执行如图的程序框图,输出的y等于( )


| A、6 | B、7 | C、8 | D、9 |
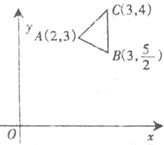 已知点(x,y)在△ABC所包围的区域内(包含边界),若B(3,
已知点(x,y)在△ABC所包围的区域内(包含边界),若B(3,| 5 |
| 2 |
A、a≥-
| ||
| B、a>0 | ||
C、a≤-
| ||
D、-
|
在△ABC中,内角A,B,C所对的边分别为a,b,c,若c2=(a-b)2+6,C=
,则△ABC的面积是( )
| 2π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
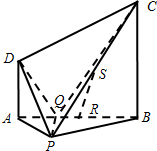 已知四棱锥P-ABCD中,底面ABCD是直角梯形,平面PAB⊥平面ABCD,R、S分别是棱AB、PC的中点,AD∥BC,AD⊥AB,PA⊥PB,AB=BC=2AD=2PA=2,
已知四棱锥P-ABCD中,底面ABCD是直角梯形,平面PAB⊥平面ABCD,R、S分别是棱AB、PC的中点,AD∥BC,AD⊥AB,PA⊥PB,AB=BC=2AD=2PA=2,