题目内容
已知函数y=2sin（2x+
）
（1）写出它的振幅、周期和初相；
（2）用五点法作出它的一个周期的图象；
（3）说明y=2sin（2x+
）的图象可由y=sinx的图象经过怎样的变换而得到？
（4）求出函数的单调增区间；
（5）求出函数图象对称轴方程和对称中心坐标．
| π |
| 3 |
（1）写出它的振幅、周期和初相；
（2）用五点法作出它的一个周期的图象；
（3）说明y=2sin（2x+
| π |
| 3 |
（4）求出函数的单调增区间；
（5）求出函数图象对称轴方程和对称中心坐标．
考点：函数y=Asin（ωx+φ）的图象变换,正弦函数的图象
专题：三角函数的图像与性质
分析：（1）由方程直接写出振幅、周期和初相；
（2）由相位分别等于0、
、π、
、2π求出x的值，描点后用平滑曲线连结得函数图象；
（3）直接运用函数图象的平移变换和伸缩变换得答案；
（4）由复合函数的单调性的求法求解函数的单调增区间；
（5）分别由相位在y轴及x轴上求得函数图象对称轴方程和对称中心坐标．
（2）由相位分别等于0、
| π |
| 2 |
| 3π |
| 2 |
（3）直接运用函数图象的平移变换和伸缩变换得答案；
（4）由复合函数的单调性的求法求解函数的单调增区间；
（5）分别由相位在y轴及x轴上求得函数图象对称轴方程和对称中心坐标．
解答：
解：（1）函数y=2sin（2x+
）的振幅是2、周期是π、初相为
；
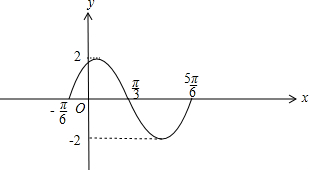
（2）列表：
描点并用平滑曲线连接，
（3）把y=sinx的图象向左平移
个单位，得到y=sin（x+
）的图象，再把所得图象上点的
纵坐标不变，横坐标缩小到原来的
，得到y=sin（2x+
）的图象，最后把所得图象上点的横坐标不变，
纵坐标扩大到原来的2倍得到y=2sin（2x+
）的图象；
（4）由-
+2kπ≤2x+
≤
+2kπ，得
-
+kπ≤x≤
+kπ，k∈Z，
∴函数的单调增区间为[-
+kπ，
+kπ]，k∈Z；
（5）由2x+
=
+kπ，得x=
+
，k∈Z，
∴函数图象对称轴方程为x=
+
，k∈Z；
由2x+
=kπ，得x=-
+
，
∴函数图象的对称中心坐标为（-
+
，0），k∈Z．
| π |
| 3 |
| π |
| 3 |
（2）列表：
| x | -
|
|
|
|
| ||||||||||
2x+
| 0 |
| π |
| 2π | ||||||||||
| y | 0 | 2 | 0 | -2 | 0 |
（3）把y=sinx的图象向左平移
| π |
| 3 |
| π |
| 3 |
纵坐标不变，横坐标缩小到原来的
| 1 |
| 2 |
| π |
| 3 |
纵坐标扩大到原来的2倍得到y=2sin（2x+
| π |
| 3 |
（4）由-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
-
| 5π |
| 12 |
| π |
| 12 |
∴函数的单调增区间为[-
| 5π |
| 12 |
| π |
| 12 |
（5）由2x+
| π |
| 3 |
| π |
| 2 |
| π |
| 12 |
| kπ |
| 2 |
∴函数图象对称轴方程为x=
| π |
| 12 |
| kπ |
| 2 |
由2x+
| π |
| 3 |
| π |
| 6 |
| kπ |
| 2 |
∴函数图象的对称中心坐标为（-
| π |
| 6 |
| kπ |
| 2 |
点评：本题考查了y=Asin（ωx+φ）型函数的图象及性质，考查了五点作图法，是基础题．
练习册系列答案
发散思维新课堂系列答案
相关题目
如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，且PA=AB=1，F为PB中点．
如图，三棱柱ABC-A1B1C1中，侧棱垂直底面，∠ACB=90°，AC=BC=