题目内容
(本小题满分12分)已知椭圆C: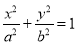 (a>b>0)的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
(a>b>0)的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
(1)求椭圆C的标准方程.
(2)设F为椭圆C的左焦点,T为直线x=-3上任意一点,过F作TF的垂线交椭圆C于点P,Q.
①证明:OT平分线段PQ(其中O为坐标原点);
②当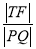 最小时,求点T的坐标.
最小时,求点T的坐标.
(1)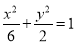 ;(2)①见解析;②(-3,1)或(-3,-1).
;(2)①见解析;②(-3,1)或(-3,-1).
【解析】
试题分析:(1)由已知可得: ,解得
,解得 ,
,
∴椭圆C的标准方程为: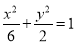 .
.
(2)①证明:由(1)可得,F的坐标为(-2,0),设T点的坐标为(-3,m),
则直线TF的斜率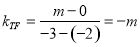 .
.
当m≠0时,直线PQ的斜率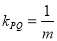 .直线PQ的方程是x=my-2.
.直线PQ的方程是x=my-2.
当m=0时,直线PQ的方程是x =-2,也符合x=my-2的形式.
设P(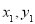 ),Q(
),Q(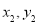 ),将直线PQ的方程与椭圆C的方程联立,得
),将直线PQ的方程与椭圆C的方程联立,得 ,
,
消去x可得: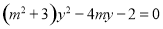 ,其判别式
,其判别式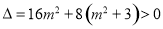 ,
,
∴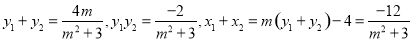 ,
,
设M为PQ中点,则M点的坐标为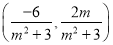 ,∴直线OM的斜率为
,∴直线OM的斜率为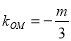 ,又直线OT的斜率
,又直线OT的斜率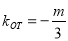 ,∴点M在直线OT上,因此OT平分线段PQ.
,∴点M在直线OT上,因此OT平分线段PQ.
②由①可得,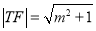 ,
,
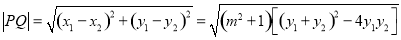
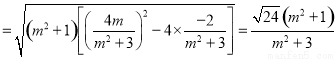 ,
,
∴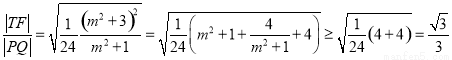 .
.
当且仅当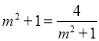 ,即m=±1,等号成立,此时
,即m=±1,等号成立,此时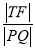 取得最小值.
取得最小值.
故当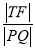 最小时,T点的坐标是(-3,1)或(-3,-1).
最小时,T点的坐标是(-3,1)或(-3,-1).
考点:椭圆的标准方程,直线与椭圆的位置关系,弦长公式
点评:利用椭圆的几何性质,求椭圆的标准方程,解决直线与椭圆的位置关系,常应用设而不求的思路解决

练习册系列答案
相关题目
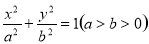 的左焦点
的左焦点 坐标为
坐标为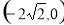 ,且椭圆C的短轴长为4,斜率为1的直线
,且椭圆C的短轴长为4,斜率为1的直线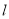 与椭圆G交于A,B两点,以AB为底边的等腰三角形,顶点为
与椭圆G交于A,B两点,以AB为底边的等腰三角形,顶点为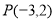 .
.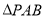 的面积
的面积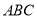 中,角
中,角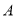
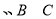 所对应的边分别为
所对应的边分别为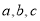 ,若
,若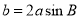 ,则角
,则角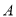 等于( )
等于( )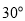 B.
B.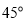 C.
C.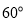 D.
D.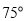
 的终边过点
的终边过点 ,那么
,那么 .
. ,则
,则 的值为( )
的值为( ) B.
B. C.
C. D.
D.
 ,
, (
( ).若
).若 是
是 的充分条件,求
的充分条件,求 的取值范围.
的取值范围. 与曲线
与曲线 有且只有一个交点,则
有且只有一个交点,则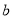 的取值范围是 ( )
的取值范围是 ( )
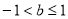 或
或
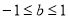 或
或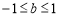
 _________.
_________. 中,顶点
中,顶点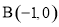 ,
,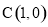 ,
,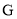 、
、 分别是
分别是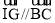 .
. 求顶点
求顶点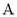 的轨迹
的轨迹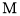 的方程;
的方程;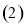 过点
过点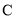 的直线交曲线
的直线交曲线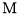 于
于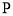 、
、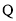 两点,
两点, 是直线
是直线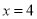 上一点,设直线
上一点,设直线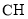 、
、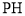 、
、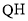 的斜率分别为
的斜率分别为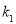 ,
,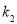 ,
,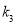 ,试比较
,试比较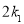 与
与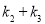 的大小,并加以证明.
的大小,并加以证明.