题目内容
(14分)已知椭圆C: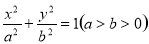 的左焦点
的左焦点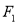 坐标为
坐标为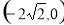 ,且椭圆C的短轴长为4,斜率为1的直线
,且椭圆C的短轴长为4,斜率为1的直线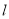 与椭圆G交于A,B两点,以AB为底边的等腰三角形,顶点为
与椭圆G交于A,B两点,以AB为底边的等腰三角形,顶点为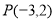 .
.
(1)求椭圆C的方程
(2)求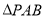 的面积
的面积
(1)  ; (2)
; (2)  .
.
【解析】
试题分析:(1) 由已知得: ,
, ,再根据公式
,再根据公式 可求得
可求得 .从而可得椭圆方程. (2) 设直线
.从而可得椭圆方程. (2) 设直线 的方程为:
的方程为: .将直线方程和椭圆方程联立消去
.将直线方程和椭圆方程联立消去 整理为关于
整理为关于 的一元二次方程.可得两根之和,两根之积.根据弦长公式可求得
的一元二次方程.可得两根之和,两根之积.根据弦长公式可求得 .
. 中点
中点 ,可得
,可得 ,即
,即 为点
为点 到直线
到直线 的距离.从而可求得
的距离.从而可求得 的面积.
的面积.
试题解析:(1)【解析】
由已知得: ,
, ,即
,即 ,所以
,所以
所以椭圆C为: 4分
4分
(2)设直线 的方程为:
的方程为:
由 得
得 6分
6分
设A,B的坐标分别为 ,
, ,AB的中点为
,AB的中点为
则 ,
, ,
, 9分
9分
又 ,
, 为
为 的中点,所以
的中点,所以
所以 ,解得
,解得 10分
10分
 ..11分
..11分
 .12分
.12分
所以 的面积
的面积 14分
14分
(如果没有介绍弦长公式,可以代入m求出A,B两点坐标算AB距离)
考点:1椭圆的方程,简单几何性质;2直线与椭圆的相交弦.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
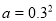 ,
, ,
,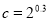 之间的大小关系是( )
之间的大小关系是( )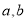 与平面
与平面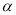 ,则下列四个命题中假命题是
,则下列四个命题中假命题是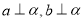 ,那么
,那么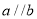 B.如果
B.如果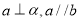 ,那么
,那么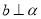
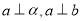 ,那么
,那么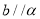 D.如果
D.如果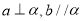 ,那么
,那么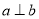
 且与
且与 有相同焦点的椭圆的方程是 .
有相同焦点的椭圆的方程是 . 的倾斜角为135;命题q:直角坐标平面内的三点A(-1,-3),B(1,1),C(2,2)共线. 则下列判断正确的是
的倾斜角为135;命题q:直角坐标平面内的三点A(-1,-3),B(1,1),C(2,2)共线. 则下列判断正确的是 为假 B.
为假 B. 为真 C.
为真 C. 为真 D.
为真 D. 为真
为真 上的点,
上的点, 分别是椭圆的左、右焦点,若
分别是椭圆的左、右焦点,若 ,则
,则 的面积为______________
的面积为______________ 在点
在点 处的切线方程是( )
处的切线方程是( ) B.
B.
 D.
D.
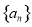 的前n项和为
的前n项和为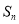 ,公差d≠0,且
,公差d≠0,且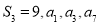 成等比数列.
成等比数列.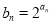 ,求数列{
,求数列{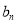 }的前n项和
}的前n项和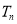 .
.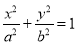 (a>b>0)的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
(a>b>0)的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.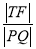 最小时,求点T的坐标.
最小时,求点T的坐标.