题目内容
在面积为1的△PMN中,tan∠M= ,tan∠N=-2,建立适当坐标系,求出以MN为焦点且过P点的椭圆方程.
,tan∠N=-2,建立适当坐标系,求出以MN为焦点且过P点的椭圆方程.
 ,tan∠N=-2,建立适当坐标系,求出以MN为焦点且过P点的椭圆方程.
,tan∠N=-2,建立适当坐标系,求出以MN为焦点且过P点的椭圆方程.椭圆方程为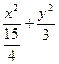 =1.
=1.
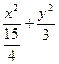 =1.
=1.如图,以MN所在直线为x轴,线段MN的垂直平分线为y轴,建立直角坐标系.
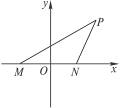
设所求椭圆方程为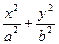 =1(a>b>0),设M、N、P的坐标分别为(-c,0)、(c,0)、(x0,y0).
=1(a>b>0),设M、N、P的坐标分别为(-c,0)、(c,0)、(x0,y0).
由题设可知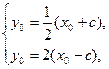 解得
解得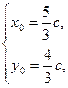 即P(
即P(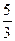 c,
c,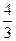 c).
c).
△MNP中,|MN|=2c,MN上的高为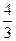 c.
c.
∴S△MNP=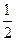 ×2c×
×2c×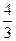 c=1.∴c=
c=1.∴c=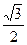 ,即P(
,即P(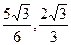 ).
).
|MP|=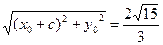 ,|NP|=
,|NP|=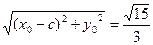 ,
,
∴a=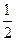 (|MP|+|NP|)=
(|MP|+|NP|)=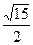 .∴b2=a2-c2=3.
.∴b2=a2-c2=3.
故所求椭圆方程为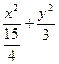 =1.
=1.

设所求椭圆方程为
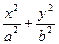 =1(a>b>0),设M、N、P的坐标分别为(-c,0)、(c,0)、(x0,y0).
=1(a>b>0),设M、N、P的坐标分别为(-c,0)、(c,0)、(x0,y0).由题设可知
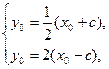 解得
解得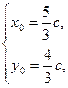 即P(
即P(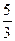 c,
c,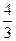 c).
c).△MNP中,|MN|=2c,MN上的高为
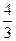 c.
c.∴S△MNP=
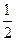 ×2c×
×2c×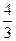 c=1.∴c=
c=1.∴c=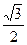 ,即P(
,即P(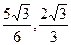 ).
).|MP|=
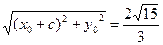 ,|NP|=
,|NP|=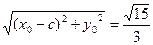 ,
,∴a=
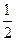 (|MP|+|NP|)=
(|MP|+|NP|)=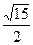 .∴b2=a2-c2=3.
.∴b2=a2-c2=3.故所求椭圆方程为
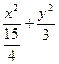 =1.
=1.
练习册系列答案
相关题目
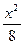 +
+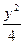 =1上求一点P,使它到定点Q(0,1)的距离最大,则P的坐标是___________.
=1上求一点P,使它到定点Q(0,1)的距离最大,则P的坐标是___________.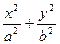 =1(a>b>0)与x轴的正半轴交于点A,O是原点.若椭圆上存在一点M,使MA⊥MO,求椭圆离心率e的取值范围.
=1(a>b>0)与x轴的正半轴交于点A,O是原点.若椭圆上存在一点M,使MA⊥MO,求椭圆离心率e的取值范围.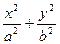 =1内有一个内接△ABC,它的一条边BC与长轴重合,A在椭圆上运动,试求△ABC重心的轨迹.
=1内有一个内接△ABC,它的一条边BC与长轴重合,A在椭圆上运动,试求△ABC重心的轨迹.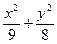 =1(x≠±3) B.
=1(x≠±3) B.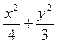 =1(y≠0) D.
=1(y≠0) D.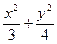 =1(y≠0)
=1(y≠0)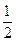 ,求顶点C的轨迹.
,求顶点C的轨迹. +
+ =1上,则( )
=1上,则( ) 与椭圆
与椭圆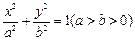 相交于
相交于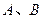 两点,且
两点,且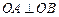 (其中
(其中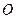 为坐标原点).(1)若椭圆的离心率为
为坐标原点).(1)若椭圆的离心率为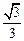 ,求椭圆的标准方程;
,求椭圆的标准方程;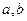 如何变化,椭圆恒过定点
如何变化,椭圆恒过定点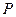
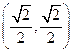 ;
;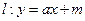 过(2)中的定点
过(2)中的定点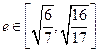 ,求原点到直线
,求原点到直线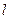 距离的取值范围.
距离的取值范围.