题目内容
.(本小题满分14分)已知直线 与椭圆
与椭圆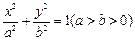 相交于
相交于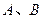 两点,且
两点,且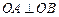 (其中
(其中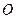 为坐标原点).(1)若椭圆的离心率为
为坐标原点).(1)若椭圆的离心率为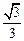 ,求椭圆的标准方程;
,求椭圆的标准方程;
(2)求证:不论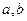 如何变化,椭圆恒过定点
如何变化,椭圆恒过定点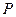
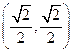 ;
;
(3)若直线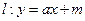 过(2)中的定点
过(2)中的定点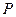 ,且椭圆的离心率
,且椭圆的离心率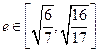 ,求原点到直线
,求原点到直线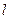 距离的取值范围.
距离的取值范围.
 与椭圆
与椭圆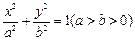 相交于
相交于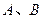 两点,且
两点,且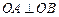 (其中
(其中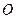 为坐标原点).(1)若椭圆的离心率为
为坐标原点).(1)若椭圆的离心率为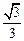 ,求椭圆的标准方程;
,求椭圆的标准方程;(2)求证:不论
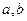 如何变化,椭圆恒过定点
如何变化,椭圆恒过定点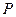
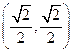 ;
;(3)若直线
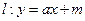 过(2)中的定点
过(2)中的定点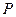 ,且椭圆的离心率
,且椭圆的离心率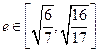 ,求原点到直线
,求原点到直线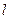 距离的取值范围.
距离的取值范围.
(Ⅰ)  (Ⅱ) (
(Ⅱ) (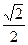 ,
,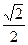 ) (Ⅲ)
) (Ⅲ)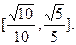
 (Ⅱ) (
(Ⅱ) (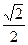 ,
,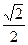 ) (Ⅲ)
) (Ⅲ)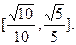
(1)由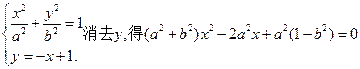
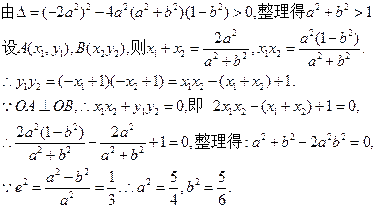
 ………5分
………5分
(2)由 则不论
则不论 如何变化,椭圆恒过第一象限内的定点(
如何变化,椭圆恒过第一象限内的定点(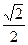 ,
,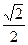 )……7分
)……7分
(3)将定点坐标代入直线方程得
则原点到直线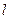 的距离为
的距离为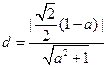 ,又
,又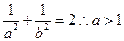 ,
,
则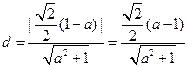 ……10分
……10分
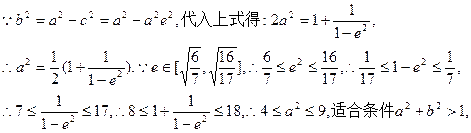
由此得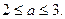 …12分 令
…12分 令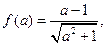
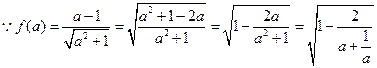 ,
,
令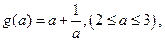 可证得
可证得
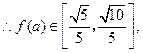

故原点到直线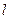 距离的取值范围为
距离的取值范围为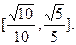 ……14分
……14分
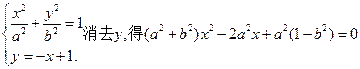
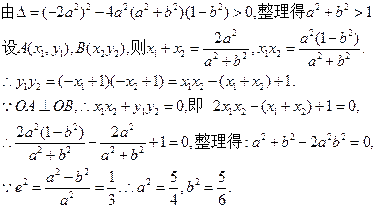
 ………5分
………5分(2)由
 则不论
则不论 如何变化,椭圆恒过第一象限内的定点(
如何变化,椭圆恒过第一象限内的定点(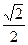 ,
,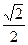 )……7分
)……7分(3)将定点坐标代入直线方程得

则原点到直线
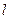 的距离为
的距离为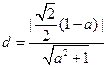 ,又
,又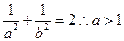 ,
,则
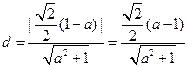 ……10分
……10分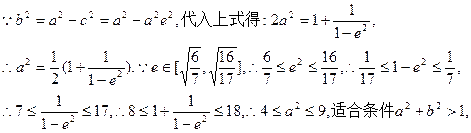
由此得
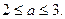 …12分 令
…12分 令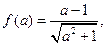
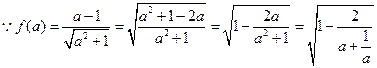 ,
,令
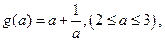 可证得
可证得
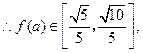

故原点到直线
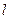 距离的取值范围为
距离的取值范围为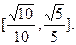 ……14分
……14分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,tan∠N=-2,建立适当坐标系,求出以MN为焦点且过P点的椭圆方程.
,tan∠N=-2,建立适当坐标系,求出以MN为焦点且过P点的椭圆方程. ,
,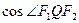 的取值范围;
的取值范围; ,试求直线PM的斜率
,试求直线PM的斜率 的范围。
的范围。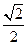 ,且椭圆经过圆C:
,且椭圆经过圆C: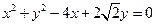 的圆心C。
的圆心C。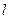 过椭圆的焦点且与圆C相切,求直线
过椭圆的焦点且与圆C相切,求直线 上任一点P,作椭圆C的右准线的垂线PH(H为垂足),延长PH到点Q,使|HQ|=λ|PH|(λ≥1)。当点P在椭圆C上运动时,点Q的轨迹的离心率的取值范围为( )
上任一点P,作椭圆C的右准线的垂线PH(H为垂足),延长PH到点Q,使|HQ|=λ|PH|(λ≥1)。当点P在椭圆C上运动时,点Q的轨迹的离心率的取值范围为( )




 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,直线y=
,直线y= x+1与椭圆相交于A、B两点,点M在椭圆上,
x+1与椭圆相交于A、B两点,点M在椭圆上, =
= +
+ ,求椭圆的方程.
,求椭圆的方程. 的左、右焦点, 三个内角A、B、C满足
的左、右焦点, 三个内角A、B、C满足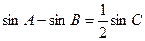 , 则顶点C的轨迹方程是( ).
, 则顶点C的轨迹方程是( ). 

 的方程;
的方程; 在
在 轴上截距的取值范围;
轴上截距的取值范围; 面积的最大值
面积的最大值


 翰林汇
翰林汇