题目内容
已知椭圆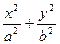 =1(a>b>0)与x轴的正半轴交于点A,O是原点.若椭圆上存在一点M,使MA⊥MO,求椭圆离心率e的取值范围.
=1(a>b>0)与x轴的正半轴交于点A,O是原点.若椭圆上存在一点M,使MA⊥MO,求椭圆离心率e的取值范围.
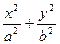 =1(a>b>0)与x轴的正半轴交于点A,O是原点.若椭圆上存在一点M,使MA⊥MO,求椭圆离心率e的取值范围.
=1(a>b>0)与x轴的正半轴交于点A,O是原点.若椭圆上存在一点M,使MA⊥MO,求椭圆离心率e的取值范围. <e<1.
<e<1.设M(x,y),则 =(x,y),
=(x,y), =(x-a,y).
=(x-a,y).
∵ ⊥
⊥ ,
,
∴0= ·
· =x(x-a)+y2.
=x(x-a)+y2.
由椭圆方程得y2=b2- x2代入得c2x2-a3x+a2b2=0.
x2代入得c2x2-a3x+a2b2=0.
解得x=a或 .
.
由题意0< <a.
<a.
∴b2<c2.∴a2-c2<c2.
解得e2= >
> .
.
∴ <e<1.
<e<1.
 =(x,y),
=(x,y), =(x-a,y).
=(x-a,y).∵
 ⊥
⊥ ,
,∴0=
 ·
· =x(x-a)+y2.
=x(x-a)+y2.由椭圆方程得y2=b2-
 x2代入得c2x2-a3x+a2b2=0.
x2代入得c2x2-a3x+a2b2=0.解得x=a或
 .
.由题意0<
 <a.
<a.∴b2<c2.∴a2-c2<c2.
解得e2=
 >
> .
.∴
 <e<1.
<e<1.
练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
 +y2=1,则与椭圆C关于直线y=x成轴对称的曲线的方程是____________.
+y2=1,则与椭圆C关于直线y=x成轴对称的曲线的方程是____________.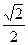 ,则
,则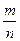 的值是________________________.
的值是________________________. 的椭圆方程是( )
的椭圆方程是( )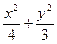 ="1"
="1"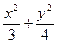 =1
=1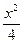 +y2="1"
+y2="1"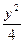 =1
=1 ,tan∠N=-2,建立适当坐标系,求出以MN为焦点且过P点的椭圆方程.
,tan∠N=-2,建立适当坐标系,求出以MN为焦点且过P点的椭圆方程. +
+ =1的左、右焦点,点P在椭圆上,△POF2是面积为
=1的左、右焦点,点P在椭圆上,△POF2是面积为 的正三角形,则b2的值为( )
的正三角形,则b2的值为( )

 的方程;
的方程; 在
在 轴上截距的取值范围;
轴上截距的取值范围; 面积的最大值
面积的最大值