题目内容
等差数列{an}的前9项和等于前4项的和,且a1=6.
(Ⅰ)求通项公式an;
(Ⅱ)求前13项和S13.
(Ⅰ)求通项公式an;
(Ⅱ)求前13项和S13.
考点:等差数列的前n项和
专题:等差数列与等比数列
分析:由已知条件利用等差数列的通项公式求出公差,由此能求出通项公式an和前13项和S13.
解答:
解:(Ⅰ)∵等差数列{an}的前9项和等于前4项的和,且a1=6,
∴9×6+
d=4×6+
d,
解得d=-1,
∴an=6+(n-1)(-1)=-n+7.
(Ⅱ)∵a1=6,d=-1,
∴S13=13×6+
×(-1)=0.
∴9×6+
| 9×8 |
| 2 |
| 4×3 |
| 2 |
解得d=-1,
∴an=6+(n-1)(-1)=-n+7.
(Ⅱ)∵a1=6,d=-1,
∴S13=13×6+
| 13×12 |
| 2 |
点评:本题考查数列的通项公式和前13项和的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知直线的倾斜角的余弦值是
,则此直线的斜率是( )
| 1 |
| 2 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、±
|
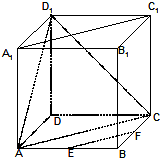 如图,棱长为2的正方体ABCD-A1B1C1D1中,点E,F分别为棱AB,BC的中点.
如图,棱长为2的正方体ABCD-A1B1C1D1中,点E,F分别为棱AB,BC的中点.