题目内容
12.已知函数f(x)=$\sqrt{3}$sinx•cosx-m•cos2x的最大值为$\frac{3}{2}$.(1)求实数m的值和函数f(x)的最小正周期;
(2)锐角△ABC的内角∠A、∠B、∠C所对的边分别为a、b、c满足f(A)=$\frac{\sqrt{3}+1}{2}$,且∠B=$\frac{π}{3}$,b=$\sqrt{6}$,求a的值.
分析 (1)由三角函数中的恒等变换应用化简函数解析式可得f(x)=$\sqrt{\frac{3+{m}^{2}}{4}}$sin(2x-φ)-$\frac{m}{2}$,其中tanφ=$\frac{\sqrt{3}m}{3}$,由$\sqrt{\frac{3+{m}^{2}}{4}}$-$\frac{m}{2}$=$\frac{3}{2}$,解得m的值,利用周期公式即可得解;
(2)由f(A)=sin(2A+$\frac{π}{6}$)+$\frac{1}{2}$=$\frac{\sqrt{3}+1}{2}$,解得:sin(2A+$\frac{π}{6}$)=$\frac{\sqrt{3}}{2}$,结合A的范围可求A的值,由正弦定理可得a的值.
解答 解:(1)∵f(x)=$\sqrt{3}$sinx•cosx-m•cos2x
=$\frac{\sqrt{3}}{2}$sin2x-$\frac{m}{2}(1+cos2x)$
=$\sqrt{\frac{3+{m}^{2}}{4}}$sin(2x-φ)-$\frac{m}{2}$,其中tanφ=$\frac{\sqrt{3}m}{3}$,
∴$\sqrt{\frac{3+{m}^{2}}{4}}$-$\frac{m}{2}$=$\frac{3}{2}$,解得m=-1,
∴f(x)=sin(2x+$\frac{π}{6}$)+$\frac{1}{2}$,最小正周期T=$\frac{2π}{2}=π$.
(2)∵f(A)=sin(2A+$\frac{π}{6}$)+$\frac{1}{2}$=$\frac{\sqrt{3}+1}{2}$,解得:sin(2A+$\frac{π}{6}$)=$\frac{\sqrt{3}}{2}$,
∵0$<A<\frac{π}{2}$,$\frac{π}{6}$<2A+$\frac{π}{6}$<$\frac{7π}{6}$,
∴2A+$\frac{π}{6}$=$\frac{π}{3}$或$\frac{2π}{3}$,解得A=$\frac{π}{12}$或$\frac{π}{4}$,
∵∠B=$\frac{π}{3}$,b=$\sqrt{6}$,
∴由正弦定理可得:a=$\frac{bsinA}{sinB}$=2或$\sqrt{4-2\sqrt{3}}$.
点评 本题主要考查了三角函数中的恒等变换应用,三角函数的周期性及其求法,考查了正弦定理的应用,属于基本知识的考查.

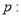 实数
实数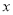 满足
满足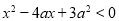 ,其中
,其中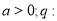 实数
实数 满足
满足 .
.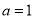 ,且
,且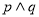 为真,求实数
为真,求实数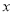 的取值范围;
的取值范围; 是
是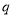 的必要不充分条件,求实数
的必要不充分条件,求实数 的取值范围.
的取值范围. ,集合
,集合 ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
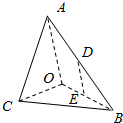 如图,在三棱锥A-BOC中,AO⊥平面COB,∠OAB=∠OAC=$\frac{π}{6}$,AB=AC=2,BC=$\sqrt{2}$,D,E分别为AB,OB的中点.
如图,在三棱锥A-BOC中,AO⊥平面COB,∠OAB=∠OAC=$\frac{π}{6}$,AB=AC=2,BC=$\sqrt{2}$,D,E分别为AB,OB的中点.