甲.乙.丙三名学生随机站成一排.则甲站在边上的概率为( )A．$\frac{1}{3}$B．$\frac{2}{3}$C．$\frac{1}{2}$D．$\frac{5}{6}$ 题目和参考答案——青夏教育精英家教网—

题目内容

9．甲，乙，丙三名学生随机站成一排，则甲站在边上的概率为（　　）

A．

$\frac{1}{3}$

B．

$\frac{2}{3}$

C．

$\frac{1}{2}$

D．

$\frac{5}{6}$

分析甲，乙，丙三名学生随机站成一排，先求出基本事件总数，再求出甲站在边上包含的基本事件个数，由此能求出甲站在边上的概率．

解答解：甲，乙，丙三名学生随机站成一排，基本事件总数n=${A}_{3}^{3}$=6，
甲站在边上包含的基本事件个数m=${C}_{2}^{1}{A}_{2}^{2}=4$，
∴甲站在边上的概率p=$\frac{m}{n}$=$\frac{4}{6}$=$\frac{2}{3}$．
故选：B．

点评本题考查概率的求法，是基础题，解题时要认真审题，注意等可能事件概率计算公式的合理运用．

练习册系列答案

20．已知{a_n}为等差数列，若$\frac{{a}_{13}}{{a}_{12}}$＜-1，且它的前n项和S_n有最大值，那么当S_n取得最小正值时，n的值为（　　）

17．设f（sinα+cosα）=sinα•cosα，则f（x）的定义域为[-$\sqrt{2}$，$\sqrt{2}$]，$f（sin\frac{π}{6}）$的值为-$\frac{3}{8}$．

4．已知函数$f（x）=\left\{{\begin{array}{l}{9，x≥3}\\{-{x^2}+6x，x＜3}\end{array}}\right.$，则不等式f（x²-2x）＜f（3x-4）的解集是（1，3）．

14．已知数列{a_n}满足a₁=3，且对任意的正整数m，n都有a_n+m=a_n•a_m，若数列{b_n}满足b_n=n-1+log₃a_n，{b_n}的前n项和为B_n．
（Ⅰ）求a_n和B_n；
（Ⅱ）令c_n=a_n•b_n，d_n=$\frac{4n+4}{{B}_{n}•{B}_{n+2}}$，数列{c_n}的前n项和为S_n，数列{d_n}的前n项和为T_n，分别求S_n和T_n．

1．

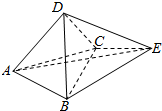如图，正三棱锥A-BCD的底面与正四面体E-BCD的侧面BCD重合，连接AE，则异面直线AE与CD所成角的大小为（　　）

18．命题?m∈[0，1]，则$x+\frac{1}{x}≥{2^m}$的否定形式是（　　）

	A．	?m∈[0，1]，则$x+\frac{1}{x}＜{2^m}$		B．	?m∈[0，1]，则$x+\frac{1}{x}≥{2^m}$
	C．	?m∈（-∞，0）∪（1，+∞），则$x+\frac{1}{x}≥{2^m}$		D．	?m∈[0，1]，则$x+\frac{1}{x}＜{2^m}$

19．若定义在区间[a，b]上的函数f（x）满足：对任意x₁，x₂∈[a，b]，都有f（$\frac{{x}_{1}+{x}_{2}}{2}$）≤$\frac{1}{2}$[f（x₁）+f（x₂）]，则称f（x）是[a，b]上的“下凸函数”，则下列说法正确的有（　　）个
①f（x）=tanx是（0，$\frac{π}{2}$）上的“下凸函数”
②无法判断f（x）=|x|+$\frac{1}{|x|}$在（-∞，0）上是否是“下凸函数”
③若f（x）=$\left\{\begin{array}{l}{{2}^{x}，x∈（-∞，0]}\\{f（x-1）+1，x∈（0，+∞）}\end{array}\right.$是（-∞，+∞）上的“下凸函数”
④若f（x）是[a，b]上的“下凸函数”，且对任意x₁，x₂，…，x₈∈[a，b]，则必有f（$\frac{{x}_{1}{x}_{2}+…+{x}_{8}}{8}$）≤$\frac{1}{8}$[f（x₁）+f（x₂）+…+f（x₈）]．

试题分类