题目内容
4.已知x=-3,x=1是函数f(x)=sin(ωx+φ)(ω>0)的两个相邻的极值点,且f(x)在x=-1处的导数f'(-1)>0,则f(0)=( )| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
分析 f(x)的周期为2×(3+1)=8,解出ω,由f(x)在x=-1处的导数f'(-1)>0,得函数f(x)在[-3,1]递增,f(1)=1,φ=2kπ+$\frac{π}{4}$,即f(0)=sin(φ)即可
解答 解:∵x=1,x=-3是函数f(x)=sin(ωx+φ)(ω>0)两个相邻的两个极值点,
∴f(x)的周期T═2×(1+3)=8,∴ω=$\frac{2π}{T}=\frac{π}{4}$,
∵f(x)在x=-1处的导数f'(-1)>0,∴函数f(x)在[-3,1]递增,
∴f(1)=1,∴ω+φ=2kπ+$\frac{π}{2}$,φ=2kπ+$\frac{π}{4}$,
f(0)=sin($\frac{π}{4}$+2kπ)=$\frac{\sqrt{2}}{2}$,
故选:D.
点评 本题考查了正弦函数的图象与性质,导数与函数单调性的关系,属于中档题

练习册系列答案
相关题目
15.△ABC的三个内角A、B、C,所对的边分别是a、b、c,若c=2$\sqrt{3}$,tanA+tanB=$\sqrt{3}$-$\sqrt{3}$tanAtanB,则△ABC的面积的取值范围是( )
| A. | [$\sqrt{3}$,+∞) | B. | (0,$\sqrt{3}$] | C. | ($\frac{1}{2}$,$\sqrt{3}$] | D. | (0,$\frac{\sqrt{3}}{2}$] |
12.△ABC的三个内角A、B、C,所对的边分别是a、b、c,若a=2,c=2$\sqrt{3}$,tanA+tanB=$\sqrt{3}$-$\sqrt{3}$tanAtanB,则△ABC的面积S△ABC=( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | 1 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
19.已知集合M={x|x<1},N={x|x(x-1)<0},则M∪N=( )
| A. | ∅ | B. | {x|0<x<1} | C. | {x|x<0} | D. | {x|x<1} |
16.已知x,y∈R,下列不等式不能恒成立的是( )
| A. | |x|≥0 | B. | x2-2x-3≥0 | C. | 2x>0 | D. | x2+y2≥2xy |
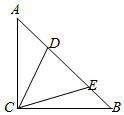 如图,等腰直角三角形区域ABC中,∠ACB=90°,BC=AC=1百米.现准备划出一块三角形区域CDE,其中D,E均在斜边AB上,且∠DCE=45°.记三角形CDE的面积为S.
如图,等腰直角三角形区域ABC中,∠ACB=90°,BC=AC=1百米.现准备划出一块三角形区域CDE,其中D,E均在斜边AB上,且∠DCE=45°.记三角形CDE的面积为S.