题目内容
已知函数f(x)＝2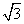
sin xcos x＋2cos2x－1(x∈R)．
(1)求函数f(x)的最小正周期及在区间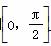
上的最大值和最小值；
(2)若f(x0)＝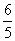
，x0∈
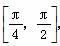，求cos 2x0的值．
解析：(1)由f(x)＝2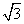sin xcos x＋2cos2x－1，得
f(x)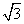＝(2sin xcos x)＋(2cos2x－1)
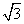＝sin 2x＋cos 2x＝2sin
，
所以函数f(x)的最小正周期为π，
因为f(x)＝2sin在区间
上为增函数，在区间
上为减函数，又f(0)＝1，f
＝2，f
＝－1，所以函数f(x)在区间
上的最大值为2，最小值为－1.
(2)由(1)可知f(x0)＝2sin
，
因为f(x0)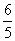＝，所以sin＝
.
由x0∈
＝－
，
所以cos 2x0＝cos
＝cos
cos 
＋sinsin
＝
.
练习册系列答案
相关题目
，B＝{(x，y)|x2＋(y－1)2≤m}，若A⊆B，则m的取值范围是________．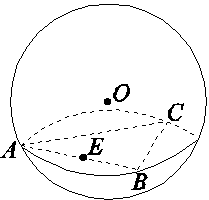
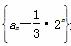是等比数列；
ω＞0)在(0,2]上恰有一个最大值1和一个最小值－1，则ω的取值范围为______．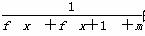
的定义域为R，求实数m的取值范围．
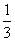AC，作直线AF与圆E相切于点F，连接EF交BC于点D，已知圆E的半径为2，∠EBC＝30°.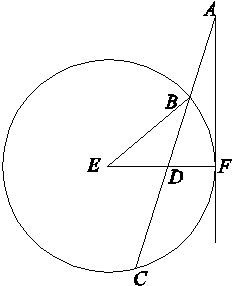
，则λ＋μ＝________．