题目内容
设函数f（x）=xex，则（ ）
| A、x=1为f（x）的极大值点 |
| B、x=1为f（x）的极小值点 |
| C、x=-1为f（x）的极大值点 |
| D、x=-1为f（x）的极小值点 |
考点：利用导数研究函数的极值
专题：导数的概念及应用
分析：由题意，可先求出f′（x）=（x+1）ex，利用导数研究出函数的单调性，即可得出x=-1为f（x）的极小值点
解答：
解：由于f（x）=xex，可得f′（x）=（x+1）ex，
令f′（x）=（x+1）ex=0可得x=-1
令f′（x）=（x+1）ex＞0可得x＞-1，即函数在（-1，+∞）上是增函数
令f′（x）=（x+1）ex＜0可得x＜-1，即函数在（-∞，-1）上是减函数
所以x=-1为f（x）的极小值点
故选：D
令f′（x）=（x+1）ex=0可得x=-1
令f′（x）=（x+1）ex＞0可得x＞-1，即函数在（-1，+∞）上是增函数
令f′（x）=（x+1）ex＜0可得x＜-1，即函数在（-∞，-1）上是减函数
所以x=-1为f（x）的极小值点
故选：D
点评：本题考查利用导数研究函数的极值，解题的关键是正确求出导数及掌握求极值的步骤，本题是基础题，
练习册系列答案
相关题目
已知 tanα＞0，cosα＜0，则角α的终边在第（ ）象限．
| A、一 | B、二 | C、三 | D、四 |
焦点坐标为（0，6），（0，-6），a=10，则此椭圆的标准方程为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
化简
•
的结果为（ ）
| -a |
| 3 | a |
A、-a
| ||
B、-(-a)
| ||
C、(-a)
| ||
D、-a
|
设m∈R，若函数f（x）=ex+2mx（x∈R）有大于零的极值点，则m的取值范围是（ ）
A、m＜-
| ||
| B、m＜0 | ||
C、m＞-
| ||
D、m＞
|
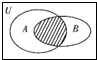设全集U=R，A={x∈Z|-2≤x≤2}，B={x∈R|x2+3x＜0}，则如图中阴影部分表示的集合为（ ）| A、{-1} |
| B、{-2，-1} |
| C、{-2，-1，0} |
| D、（-2，-1） |
在等差数列{an}中，a1=1，a4=7，则公差d为（ ）
| A、4 | B、6 | C、1 | D、2 |
若A（x，1-x，2x），B（1，-2，x-1），当|
|取最小值时，x的值等于（ ）
| AB |
| A、1 | B、0 | C、-2 | D、-1 |