题目内容
8.设等差数列{an}的前n项和为Sn.已知(a2-1)3+2013(a2-1)=1,(a2012-1)3+2013(a2012-1)=-1,则S2013等于( )| A. | 1006 | B. | 1007 | C. | 2012 | D. | 2013 |
分析 由已知条件推导出a2+a2012=2,由此能求出S2013的值.
解答 解:∵等差数列{an}的前n项和为Sn.
(a2-1)3+2013(a2-1)=1,(a2012-1)3+2013(a2012-1)=-1,
∴(a2-1)3+2013(a2-1)+(a2012-1)3+2013(a2012-1)=0,
整理可得(a2+a2012-2)•[(a2-1)2+(a2012-1)2-(a2-1)(a2012-1)+2013]=0,
∵由(a2-1)3+2013(a2-1)=1,(a2012-1)3+2013(a2012-1)=-1
∴a2-1>0,-1<a2012-1<0,即a2>1,0<a2012<1,从而可得等差数列的公差d<0
∴(a2-1)2+(a2012-1)2-(a2-1)(a2012-1)+2013>0,
∴a2+a2012=2,
∴S2013=$\frac{2013}{2}({a}_{1}+{a}_{2013})$=$\frac{2013}{2}({a}_{2}+{a}_{2012})$=$\frac{2013}{2}×2$=2013.
故选:D.
点评 本题考查等差数列的前2013项和的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
18.命题“若x=1,则x2-1=0”的否命题是( )
| A. | 若x=1,则x2-1≠0 | B. | 若x≠1,则x2-1=0 | C. | 若x≠1,则x2-1≠0 | D. | 若x2-1≠0,则x≠1 |
16.设函数f(3x+2)=9x+5,则f(x)的表达式是( )
| A. | 3x+1 | B. | 9x-1 | C. | 3x-1 | D. | 9x+1 |
10.已知集合A={x∈R|x≤1},B={x∈R|x2≤4},A∩B=( )
| A. | (-∞,2] | B. | [-2,2] | C. | [1,2] | D. | [-2,1] |
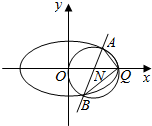 如图,已知焦点在x轴上的椭圆C过点(-2,0),且离心率为$\frac{\sqrt{3}}{2}$,Q为椭圆C的右顶点.
如图,已知焦点在x轴上的椭圆C过点(-2,0),且离心率为$\frac{\sqrt{3}}{2}$,Q为椭圆C的右顶点.