题目内容
椭圆x2+4y2=36的弦被(4,2)平分,则此弦所在直线方程为 .
考点:直线与圆锥曲线的关系
专题:圆锥曲线的定义、性质与方程
分析:设弦的端点坐标为(x1,y1),(x2,y2),则x1+x2=8,y1+y2=4,代入椭圆方程可得,x12+4y12=36,x22+4y22=36,两个方程作差可求得直线斜率,利用点斜式可得直线方程,注意检验.
解答:
解:设弦的端点坐标为(x1,y1),(x2,y2),则x1+x2=8,y1+y2=4,
代入椭圆方程可得,x12+4y12=36,①,
x22+4y22=36②
①-②得,(x1+x2)(x1-x1)+4(y1+y2)(y1-y2)=0
∴
=-
=-
,
由点斜式方程可得直线方程为:y-2=
(x-4),即x+2y-8=0,
经检验符合题意,
故答案为:x+2y-8=0.
代入椭圆方程可得,x12+4y12=36,①,
x22+4y22=36②
①-②得,(x1+x2)(x1-x1)+4(y1+y2)(y1-y2)=0
∴
| y1-y2 |
| x1-x2 |
| x1+x2 |
| 4(y1+y2) |
| 1 |
| 2 |
由点斜式方程可得直线方程为:y-2=
| 1 |
| 2 |
经检验符合题意,
故答案为:x+2y-8=0.
点评:本题考查直线与椭圆的位置关系,属中档题,涉及弦中点问题常采取“平方差法”解决.

练习册系列答案
相关题目
已知角α的终边经过点P(-1,3),则sinα-2cosα=( )
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
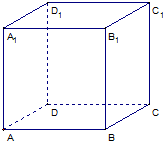 如图,在正方体ABCD-A1B1C1D1中,E,F分别为AB、AD的中点,
如图,在正方体ABCD-A1B1C1D1中,E,F分别为AB、AD的中点,