题目内容
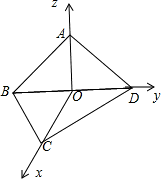
 菱形ABCD中,AB=2,∠BCD=60°,现将其沿对角线BD折成直二面角A-BD-C(如图),则异面直线AB与CD所成角的余弦值为
菱形ABCD中,AB=2,∠BCD=60°,现将其沿对角线BD折成直二面角A-BD-C(如图),则异面直线AB与CD所成角的余弦值为
- A.

- B.

- C.

- D.

C
分析:设O为BD中点,连接OA,OC,可以证明OA,OC,OD两两垂直,以O为坐标原点,建立空间直角坐标系,利用向量方法求出异面直线AB与CD所成角的余弦值.
解答:设O为BD中点,连接OA,OC,由已知,△BCD,△BAD均为正三角形,∴CO⊥BD,AO⊥BD,则∠AOC为二面角A-BD-C的平面角,∠AOC=90°,
即AO⊥OC.以O为坐标原点,建立空间直角坐标系.
设AB=2,则AO=CO= ,所以A( 0,0,
,所以A( 0,0, ) B(0,-1,0)C(
) B(0,-1,0)C( ,0,0)D(0,1,0),
,0,0)D(0,1,0), =(-
=(- ,1,0),
,1,0), =(0,-1,-
=(0,-1,- )
)
cos< ,
, >=
>=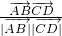 =-
=- .∴异面直线AB与CD所成角的余弦值为
.∴异面直线AB与CD所成角的余弦值为 .
.
故选C.
点评:本题考查异面直线夹角求解,利用向量的方法,能降低了思维难度.注意一般地异面直线所成角与两直线方向向量夹角相等或互补,余弦的绝对值相等.
分析:设O为BD中点,连接OA,OC,可以证明OA,OC,OD两两垂直,以O为坐标原点,建立空间直角坐标系,利用向量方法求出异面直线AB与CD所成角的余弦值.
解答:设O为BD中点,连接OA,OC,由已知,△BCD,△BAD均为正三角形,∴CO⊥BD,AO⊥BD,则∠AOC为二面角A-BD-C的平面角,∠AOC=90°,
即AO⊥OC.以O为坐标原点,建立空间直角坐标系.

设AB=2,则AO=CO=
 ,所以A( 0,0,
,所以A( 0,0, ) B(0,-1,0)C(
) B(0,-1,0)C( ,0,0)D(0,1,0),
,0,0)D(0,1,0), =(-
=(- ,1,0),
,1,0), =(0,-1,-
=(0,-1,- )
)cos<
 ,
, >=
>=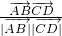 =-
=- .∴异面直线AB与CD所成角的余弦值为
.∴异面直线AB与CD所成角的余弦值为 .
.故选C.
点评:本题考查异面直线夹角求解,利用向量的方法,能降低了思维难度.注意一般地异面直线所成角与两直线方向向量夹角相等或互补,余弦的绝对值相等.

练习册系列答案
相关题目

 (2007•盐城一模)菱形ABCD中,AB=2,∠BCD=60°,现将其沿对角线BD折成直二面角A-BD-C(如图),则异面直线AB与CD所成角的余弦值为( )
(2007•盐城一模)菱形ABCD中,AB=2,∠BCD=60°,现将其沿对角线BD折成直二面角A-BD-C(如图),则异面直线AB与CD所成角的余弦值为( )